Clase 1 Introducción

1.1 ¿Qué es aprendizaje de máquina (machine learning)?

Métodos computacionales para aprender de datos con el fin de producir reglas para mejorar el desempeño en alguna tarea o toma de decisión.

En este curso nos enfocamos en las tareas de aprendizaje supervisado (predecir o estimar una variable respuesta a partir de datos de entrada) y aprendizaje no supervisado (describir estructuras interesantes en datos, donde no necesariamente hay una respuesta que predecir).

Ejemplos de tareas de aprendizaje:

• Predecir si un cliente de tarjeta de crédito va a caer en impago en los próximos tres meses.
• Reconocer palabras escritas a mano (OCR).
• Detectar llamados de ballenas en grabaciones de boyas.
• Estimar el ingreso mensual de un hogar a partir de las características de la vivienda, posesiones y equipamiento y localización geográfica.
• Dividir a los clientes de Netflix según sus gustos.
• Recomendar artículos a clientes de un programa de lealtad o servicio online.

Las razones usuales para intentar resolver estos problemas computacionalmente son diversas:

• Quisiéramos obtener una respuesta barata, rápida, automatizada, y con suficiente precisión. Por ejemplo, reconocer caracteres en una placa de coche de una fotografía se puede hacer por personas, pero eso es lento y costoso. Igual oír cada segundo de grabación de las boyas para saber si hay ballenas o no. Hacer mediciones directas del ingreso de un hogar requiere mucho tiempo y esfuerzo.
• Quisiéramos superar el desempeño actual de los expertos o de reglas simples utilizando datos: por ejemplo, en la decisión de dar o no un préstamo a un solicitante, puede ser posible tomar mejores decisiones con algoritmos que con evaluaciones personales o con reglas simples que toman en cuenta el ingreso mensual, por ejemplo.
• Al resolver estos problemas computacionalmente tenemos oportunidad de aprender más del problema que nos interesa: estas soluciones forman parte de un ciclo de análisis de datos donde podemos aprender de una forma más concentrada cuáles son características y patrones importantes de nuestros datos.

Es posible aproximarse a todos estos problemas usando reglas (por ejemplo, si los pixeles del centro de la imagen están vacíos, entonces es un cero, si el crédito total es mayor al 50% del ingreso anual, declinar el préstamo, etc). Las razones para no tomar un enfoque de reglas construidas “a mano”:

• Cuando conjuntos de reglas creadas a mano se desempeñan mal (por ejemplo, para otorgar créditos, reconocer caracteres, etc.)

• Reglas creadas a mano pueden ser difíciles de mantener (por ejemplo, un corrector ortográfico), pues para problemas interesantes muchas veces se requieren grandes cantidades de reglas. Por ejemplo: ¿qué búsquedas www se enfocan en dar direcciones como resultados? ¿cómo filtrar comentarios no aceptables en foros?

1.2 Ejemplo: reglas y aprendizaje

Lectura de un medidor mediante imágenes. Supongamos que en una infraestructura donde hay medidores análogos (de electricidad, gas, etc.) que no se comunican. ¿Podríamos pensar en utilizar fotos tomadas automáticamente para medir el consumo?

Por ejemplo, consideramos el siguiente problema (tomado de este sitio):

library(imager)
library(tidyverse)
# Datos: http://raphael.candelier.fr/?blog=Image%20Moments
medidor_vid <- load.video("figuras/gauge_raw.mp4", fps = 5)

Nótese que las imágenes y videos son matrices o arreglos de valores de pixeles, por ejemplo estas son las dimensiones para el video y para un cuadro:

dim(medidor_vid)

## [1] 370 336  70   3

medidor <- frame(medidor_vid, 20)
dim(medidor)

## [1] 370 336   1   3

En este caso, el video tienen 350 cuadros, y existen tres canales. Cada canal está representado por una matriz de 370x336 valores, y en cada uno está un valor que representa la intensidad del pixel.

Buscámos hacer cálculos con estas matrices para extraer la información que queremos. En este caso, construiremos estos cálculos a mano.

Primero filtramos (extraemos canal rojo, difuminamos y aplicamos un umbral):

medidor_1 <- medidor %>% R %>% isoblur(10)
aguja <-  medidor_1 %>% threshold("99%")

Logramos extraer la aguja, aunque hay algo de ruido adicional. Podemos extraer las líneas que pasan por más pixeles encendidos (transformada de Hough). Con estas líneas tenemos calculada la orientación de la aguja:

lineas_h <- hough_line(aguja, ntheta = 500, data.frame = T)
lineas_top <- lineas_h %>% 
    arrange(desc(score)) %>% 
    top_n(5) %>% 
    select(-score)  
lineas_top

##      theta        rho
## 1 2.354621 -21.519296
## 2 2.354621 -23.521298
## 3 5.502509  24.531202
## 4 2.266480  -4.377799
## 5 2.279071  -7.398547

Y ahora podemos aplicar el proceso de arriba a todas la imágenes:

seleccionar_lineas <- function(lineas){
    lineas %>% 
      arrange(desc(score)) %>% 
      filter(rho > 0) %>% 
      top_n(5, score) %>% 
      select(-score) %>% 
      summarise(theta = 180*mean(theta)/pi) %>% 
      pull(theta)
}

# procesar por cuadro
num_cuadros <- dim(medidor_vid)[3]

angulos <- 1:num_cuadros %>% 
    map( ~frame(medidor_vid, .x)) %>% 
    map(R) %>% map( ~ isoblur(.x, 10)) %>% 
    map( ~ threshold(.x, "98%")) %>% 
    map( ~ hough_line(.x, 100, data.frame = TRUE)) %>% 
    map_dbl(seleccionar_lineas)

angulos_tbl <- tibble(t = 1:num_cuadros, angulo = angulos)

# puedes usar este código para crear un gif animado:
library(gganimate)
ggplot(angulos_tbl, aes(x = t, y = angulo)) +
    geom_line() +
    transition_reveal(t) 

---

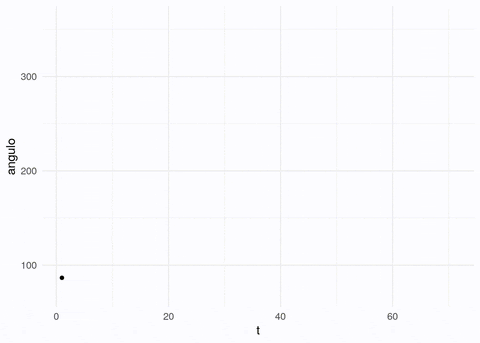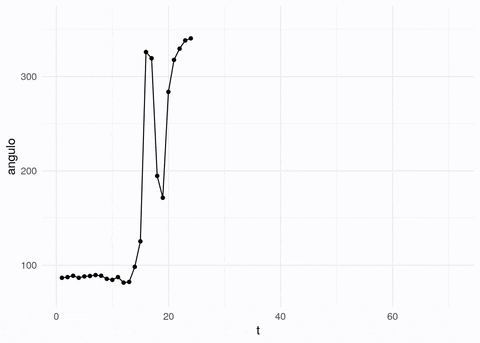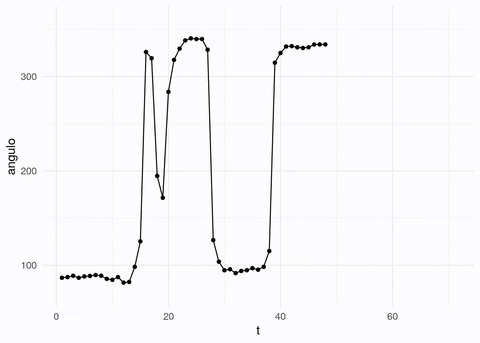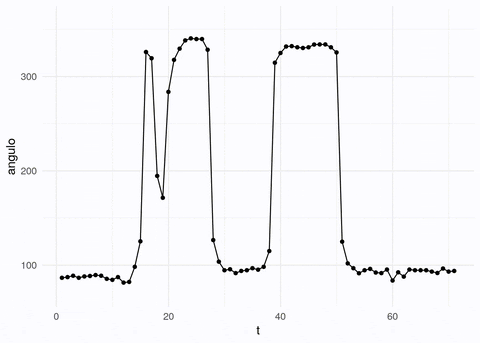
Por el contrario, en el enfoque de aprendizaje, comenzamos con un conjunto de datos etiquetado (por una persona, por un método costoso, etc.), y utilizamos alguna estructura general para aprender a producir la respuesta a partir de las imágenes. Por ejemplo, en este caso podríamos usar regresión lineal (regularizada) sobre los valores de los pixeles de la imagen:

library(keras)
# usamos los tres canales de la imagen
x <- as.array(medidor_vid) %>% aperm(c(3,1,2,4))

# reordenamos
set.seed(12334)
orden <- sample(1:num_cuadros, num_cuadros)
x <- x[orden,,,,drop=FALSE]
y <- angulos[orden]

modelo_aguja <- keras_model_sequential() %>%
    layer_flatten() %>% 
    layer_dropout(rate = 0.9) %>% 
    layer_dense(units = 1, activation = 'linear')

Ajustamos el modelo:

modelo_aguja %>% compile(
  loss = loss_mean_absolute_error,
  optimizer = optimizer_sgd(lr = 0.01, decay = 0.001),
  metrics = c('mean_absolute_error')
)
# Entrenar
modelo_aguja %>% fit(
  x, y,
  batch_size = 25,
  epochs = 150,
  validation_split = 0.1,
  verbose = FALSE
)

Y observamos que obtenemos predicciones prometedoras:

preds <- predict(modelo_aguja, x)
preds_tbl <- tibble(y = y, preds = preds)
ggplot(preds_tbl, aes(x = preds, y = y)) +
  geom_point(alpha = 0.5) +
  geom_abline(colour = 'red')

De forma que podemos resolver este problema con algoritmos generales, como regresión, sin tener que aplicar métodos sofisticados de procesamiento de imágenes. El enfoque de aprendizaje es particularmente efectivo cuando hay cantidades grandes de datos poco ruidosos, y aunque en este ejemplo los dos enfoques dan resultados razonables, en procesamiento de imágenes es cada vez más común usar redes neuronales grandes para resolver este tipo de problemas.

1.3 Ejemplo: mediciones costosas

Consideramos la medición de ingreso total trimestral para los hogares de la encuesta ENIGH. Cada una de estas mediciones es muy costosa en tiempo y dinero. Sin embargo, hay otras características de los hogares que podemos medir.

Por ejemplo, consideremos una muestra de la ENIGH 2010:

dat_ingreso <- read_csv(file = '../datos/enigh-ejemplo.csv') %>% 
  mutate(num_focos = FOCOS) %>%
  mutate(ingreso_miles = round(INGCOR / 1000)) %>% 
  mutate(tel_celular = ifelse(SERV_2 == 1, "Sí", "No")) %>% 
  mutate(marginación = fct_reorder(marginación, ingreso_miles, median)) %>% 
  rename(ocupadas = PEROCU)

sample_n(dat_ingreso, 10) %>% 
    select(entidad = NOM_ENT, num_focos, marginación, 
           tel_celular, ocupadas, ingreso_miles)  %>%
    arrange(desc(ingreso_miles)) %>% 
    knitr::kable()

entidad	num_focos	marginación	tel_celular	ocupadas	ingreso_miles
Tabasco	10	Muy bajo	Sí	2	68
Nayarit	10	Muy bajo	Sí	1	47
Distrito Federal	7	Muy bajo	Sí	2	45
Nayarit	11	Bajo	Sí	1	41
Guanajuato	3	Medio	No	2	27
Hidalgo	6	Muy bajo	Sí	0	22
Distrito Federal	6	Muy bajo	Sí	1	16
Jalisco	3	Muy bajo	Sí	2	15
Yucatán	19	Muy bajo	Sí	1	15
Nuevo León	3	Alto	No	1	9

Estos son algunos percentiles sobre toda la muestra:

quantile(dat_ingreso$ingreso_miles, probs= c(0.05, 0.10,0.5,0.9, 0.95)) %>% round(2)

##  5% 10% 50% 90% 95% 
##   6   8  23  62  83

Quizá podemos usar otras variables más fácilmente medibles para predecir el ingreso de un hogar. Por ejemplo, podríamos considerar variables de entorno (marginación del municipio), del hogar (si tienen celular), y de las personas dentro del hogar (número de personas ocupadas):

ggplot(dat_ingreso, 
       aes(x = ocupadas, y = ingreso_miles, colour= tel_celular)) + 
  geom_jitter(width=0.5, height = 0.3, size = 1, alpha = 0.5) +
  scale_y_log10(breaks = c(2.5, 5, 10, 20, 40, 80, 160, 320), 
                limits = c(2.5, 360)) +
    ylab("Ingreso trimestral \n (miles de pesos)") +
  facet_wrap( ~marginación, nrow=1) + 
  geom_smooth(span = 5, method = "loess", method.args = list(degree=1)) +
  xlab("Personas ocupadas")

ggplot(dat_ingreso, 
       aes(x = num_focos, y = (0.1 + ingreso_miles) / (TOT_RESI - MENORES), colour = tel_celular)) + 
  geom_jitter(width=0.5, size=1, alpha = 0.5) +
  scale_y_log10(breaks = c(2.5, 5, 10, 20, 40, 80), limits = c(1.5, 100)) +
    ylab("Ingreso trimestral por adulto \n (miles de pesos)") +
  facet_wrap( ~marginación, nrow=1) + 
  geom_smooth(span = 5, method = "loess", method.args = list(degree=1, family = "symmetric")) +
  xlab("Número de focos") + xlim(c(0,25))

Estas variables son relevantes, y vemos que explican una parte considerable de la variación de los ingresos de los hogares. Sin embargo, ¿cómo podemos mejorar nuestras predicciones para el estrato de marginación muy alta, donde hay relativamente pocos datos, o para aquellos hogares con alto número de focos? Parece ser necesario incluir más variables.

• En algunas encuestas se pregunta directamente el ingreso mensual del hogar. La respuesta es generalmente una mala estimación del verdadero ingreso, por lo que actualmente se prefiere utilizar aprendizaje para estimar a partir de otras variables que son más fielmente reportadas por encuestados (años de estudio, ocupación, número de focos en el hogar, etc.)

1.4 Aprendizaje supervisado y no supervisado

Las tareas de aprendizaje se dividen en dos grandes partes: aprendizaje supervisado y aprendizaje no supervisado.

En Aprendizaje supervisado buscamos construir un modelo o algoritmo para predecir o estimar un target o una respuesta a partir de ciertas variables de entrada.

Predecir y estimar, en este contexto, se refieren a cosas similares. Generalmente se usa predecir cuando se trata de variables que no son observables ahora, sino en el futuro, y estimar cuando nos interesan variables actuales que no podemos observar ahora por costos o por la naturaleza del fenómeno.

Por ejemplo, para identificar a los clientes con alto riesgo de impago de tarjeta de crédito, utilizamos datos históricos de clientes que han pagado y no han pagado. Con estos datos entrenamos un algoritmo para detectar anticipadamente los clientes con alto riesgo de impago.

Usualmente dividimos los problemas de aprendizaje supervisado en dos tipos, dependiendo de la variables salida:

• Problemas de regresión: cuando la salida es una variable numérica. El ejemplo de estimación de ingreso es un problema de regresión
• Problemas de clasificación: cuando la salida es una variable categórica. El ejemplo de detección de dígitos escritos a manos es un problema de clasificación.

En contraste, en Aprendizaje no supervisado no hay target o variable respuesta. Buscamos modelar y entender las relaciones entre variables y entre observaciones, o patrones importantes o interesantes en los datos.

Los problemas supervisados tienen un objetivo claro: hacer las mejores predicciones posibles bajo ciertas restricciones. Los problemas no supervisados tienden a tener objetivos más vagos, y por lo mismo pueden ser más difíciles.

1.5 Predicciones y su evaluación

Por el momento nos concentramos en problemas supervisados de regresión, es decir predicción de variables numéricas. ¿Cómo entendemos el problema de predicción?

Proceso generador de datos

Pensaremos en términos de procesos usualmente estocásticos que generan los datos. Supongamos que nos interesa predecir una variable respuesta \(Y\) numérica en términos de variables de entrada disponibles \(x = (x_1,x_2,\ldots, x_p)\). Dadas las variables de entrada, observamos una salida:

\[(x_1, x_2, \ldots, x_p) \to y\]

y queremos predecir, para cada juego de entradas dado, qué valor de salida vamos a observar. El proceso que produce la salida \(y\) a partir de las entradas es típicamente muy complejo y dificíl de describir de forma mecanística (por ejemplo, el ingreso dadas características de los hogares). En muchos casos, tiene sentido pensar que estos modelo son estocásticos y no deterministas, pues puede haber muchas otras variables no medidas (no incluidas en nuestras \(x_i\)’s) que influyen sobre \(y\).

Nuestro primer propósito es construir una función \(f\) tal que si observamos cualquier \((x_1, x_2, \ldots, x_p) \to y\), entonces nuestra predicción es

\[\hat{y} = f(x_1, x_2, \ldots, x_p)\] Y buscamos que en cada caso \(f(x_1, x_2 \ldots, x_p) \approx y\), es decir, con una regla o algoritmo \(f\) podemos predecir con buena precisión el valor de \(y\). Esta \(f\), como explicamos antes, puede ser producida de muy distintas maneras (experiencia, reglas a mano, datos, etc.) En cualquier caso, nuestra primera tarea es definir qué quiere decir predecir con buena precisión.

Distintos problemas tendrán distintas maneras de definir qué es una buena predicción, que también depende de cuál es la razón por la que construimos estos modelos.

Ejemplo

Para predecir el precio de venta de una casa en el mercado usamos la función

\[ f(x) = f(m2, calidad) = (10000 + 500 * calidad ) * m^2 \]

donde m^2 es el área de las casas, y calidad es una calificación de los terminados de la casa. ¿Cómo mediríamos el desempeño de esta regla?

Datos de prueba y función de pérdida

La respuesta más directa es: tomamos una muestra de casas que se han vendido recientemente y registramos su precio de venta (ventas que ocurrieron típicamente después de que construimos la función \(f\):

\[{\mathcal T} = \{(\mathbf{x}^{(1)}, \mathbf{y}^{(1)}), (\mathbf{x}^{(2)}, \mathbf{y}^{(2)}), \ldots, (\mathbf{x}^{(m)}, \mathbf{y}^{(m)})\},\]

Compararíamos entonces las respuestas observadas \(\mathbf{y^{(i)}}\) con las predicciones \(f(\mathbf{x^{(i)}})\). ¿Las diferencias son muy grandes? ¿subestimamos o sobrestimamos mucho?, etc ).

Más precisamente, comparamos observados con las predicciones de \(f\) con una función de pérdida. En este caso, por ejemplo, podríamos usar

\[L \left(f(\mathbf{x}^{(i)}), \mathbf{y}^{(i)}\right ) = \left |\mathbf{y}^{(i)} - f(\mathbf{x}^{(i)})\right |\]

que es valor absoluto de la diferencia entre el precio de venta observado y el nuestra predicción. Pero quizá nos interese por conveniencia más el error cuadrático:

\[L \left (f(\mathbf{x}^{(i)}), \mathbf{y}^{(i)}\right ) =\left(\mathbf{y}^{(i)} - f(\mathbf{x}^{(i)})\right )^2\]

A la función \(L\) le llamamos la función de pérdida, y con ella evaluamos el tamaño de los errores de predicción.

Obsérvese que en general es posible que para algunos casos tengamos errores grandes pero que en general el comportamiento sea adecuado, y eso no querría decir necesariamente que nuestra regla \(f\) es un mal predictor en general. Una idea simple es resumir evaluando el error promedio sobre los datos de prueba. El error de prueba de \(f\) es

\[ \widehat{Err}(f) = \frac{1}{m} \sum_{i=1}^m L(\mathbf{y}^{(i)} , f(\mathbf{x}^{(i)}))\] Por ejemplo, si usamos la pérdida absoluta,

\[ \widehat{Err}(f) = \frac{1}{m} \sum_{i=1}^m |\mathbf{y}^{(i)} - f(\mathbf{x}^{(i)})|\] o la cuadrática:

\[ \widehat{Err}(f) = \frac{1}{m} \sum_{i=1}^m (\mathbf{y}^{(i)} - f(\mathbf{x}^{(i)}))^2\] Aunque podríamos usar también error relativo u otra medida más interpretable o apropiada para nuestro problema. A esta última cantidad le llamamos error de prueba. A los datos que usamos para calcularla le llamamos el conjunto de datos de prueba.

Ejemplo

Para la función que mostramos arriba que quisiéramos usar para predecir precios de ventas de casas, usando la pérdida absoluta tendríamos:

f <- function(m2, calidad){
  (10000 + 500 * calidad ) * m2 
}
L <- function(y, pred){
  abs(y - pred)
}

Una vez que tenemos \(f\), podemos recolectar una muestra de prueba de casas que se han vendido recientemente (en este caso 100 casas):

datos_prueba %>% head()

## # A tibble: 6 x 3
##      m2 calidad   precio
##   <dbl>   <int>    <dbl>
## 1 245.       10  3969300
## 2 784.        3  7950800
## 3 668.        9 10395500
## 4  83.5       5   998700
## 5 921.        9 13947400
## 6 450.        8  6065000

Y evaluamos el error de prueba:

datos_prueba %>% 
  mutate(pred = f(m2, calidad)) %>% #calcular predicción
  mutate(perdida_abs = L(precio, pred)) %>% #calcular pérdida
  summarise(predida_prueba = mean(perdida_abs) %>% round(2)) # promediar

## # A tibble: 1 x 1
##   predida_prueba
##            <dbl>
## 1        292993.

Este es el error promedio que esperamos cuando usamos este predictor. En este ejemplo, nos podría también interesar calcular el error relativo, que introduce una medida de pérdida distinta:

L_relativa <- function(y, pred){
  100 * abs(y - pred) / pred
}
datos_prueba %>% 
  mutate(pred = f(m2, calidad)) %>% #calcular predicción
  mutate(perdida_abs = L_relativa(precio, pred)) %>% #calcular pérdida
  summarise(predida_prueba = mean(perdida_abs) %>% round(2)) # promediar

## # A tibble: 1 x 1
##   predida_prueba
##            <dbl>
## 1           6.92

---

En el caso donde los datos de prueba son una muestra (datos independientes e identicamente distribuidos) extraida del proceso generador de datos, esta cantidad estima el error predictivo:

\[ Err(f) = E_{(x,y)}\left( L(y, f(x))\right ) \] donde el valor esperado es sobre la distribución conjunta de \((x, y) \sim \pi\). Nótese que esta es una cantidad teórica que tenemos que estimar. Si la muestra de prueba es suficientemente grande ( \(m\) es grande ), entonces

\[ \widehat{Err}(f) = \frac{1}{m} \sum_{i=1}^m L(\mathbf{y}^{(i)} , f(\mathbf{x}^{(i)})) \approx Err(f)\] Observación: nótese que para que este argumento funcione, la \(f\) no puede depender de ninguna manera de los datos de prueba \((\mathbf{x}^{(1)}, \mathbf{y}^{(1)}), (\mathbf{x}^{(2)}, \mathbf{y}^{(2)}), \ldots, (\mathbf{x}^{(m)}, \mathbf{y}^{(m)}),\) pues entonces tendríamos que tomar el valor esperado promediando sobre \(f\), y esta promedio no estima \(Err(f)\)

• Nuestro propósito principal es encontrar una \(f\) para predecir que minimice el error predictivo
• En la práctica, buscamos valores chicos del error de prueba \(\widehat{Err}\) (que aproxima al error predictivo).
• La \(f\) no puede depender de ninguna manera de los datos de prueba.

1.6 Tarea fundamental del aprendizaje supervisado

En aprendizaje supervisado, buscamos construir la función \(f\) de manera automática usando datos. Supongamos entonces que tenemos un conjunto de datos etiquetados (sabemos la \(y\) correspondiente a cada \(x\)):

\[{\mathcal L}=\{ (x^{(1)},y^{(1)}),(x^{(2)},y^{(2)}), \ldots, (x^{(N)}, y^{(N)}) \}\]

que llamamos conjunto de entrenamiento.

Un algoritmo de aprendizaje (aprender de los datos) es una regla que asigna a cada conjunto de entrenamiento \({\mathcal L}\) una función \(\hat{f}\):

\[{\mathcal L} \to \hat{f}.\]

Una vez que construimos la función \(\hat{f}\), podemos hacer predicciones. El desempeño del predictor particular \(\hat{f}\) se mide como sigue: si en el futuro observamos otra muestra \({\mathcal T}\), que llamamos muestra de prueba,

\[{\mathcal T} = \{(\mathbf{x}^{(1)}, \mathbf{y}^{(1)}), (\mathbf{x}^{(2)}, \mathbf{y}^{(2)}), \ldots, (\mathbf{x}^{(m)}, \mathbf{y}^{(m)})\},\]

entonces decimos que el error de predicción (cuadrático) de \(\hat{f}\) para el ejemplo \((\mathbf{x^{(j)}},\mathbf{y}^{(j)})\) está dado por \[L(\mathbf{y}^{(j)} , \hat{f}(\mathbf{x}^{(j)}))\]

y el error promedio sobre la muestra \({\mathcal T}\) es

\[ \widehat{Err}(f) = \frac{1}{m} \sum_{i=1}^m L(\mathbf{y}^{(i)} , f(\mathbf{x}^{(i)})) \]

que es una estimación del error de predicción \(Err\)

Adicionalmente, definimos otra cantidad de menor interés, el error de entrenamiento, como

\[\overline{err} = \frac{1}{N}\sum_{i=1}^N L(y^{(i)} , \hat{f}(x^{(i)})).\]

La tarea fundamental del análisis supervisado es:

• Usando datos de entrenamiento \({\mathcal L}\), construimos una funcion \(\hat{f}\) para predecir
• Si observamos nuevos valores \(x_0\), nuestra predicción es \(\hat{y} = \hat{f}(x_0)\).
• Buscamos que cuando observemos nuevos casos para predecir, nuestro error de predicción sea bajo en promedio (\(Err\) sea bajo)
• Usualmente estimamos \(Err\) mediante una muestra de prueba o validación \({\mathcal T}\), así que buscamos minimizar la estimación \(\hat{Err}\)
• Nos interesan métodos de construir \(\hat{f}\) que produzcan errores de predicción bajos.

Nótese que el error de entrenamiento se calcula sobre la muestra \({\mathcal L}\) que se usó para construir \(\hat{f}\), mientras que el error de predicción se estima usando una muestra independiente \({\mathcal T}\).

\(\hat{Err}\) es una estimación razonable de el error de predicción \(Err\) (por ejemplo, \(\hat{Err} \to Err\) cuando el tamaño de la muestra de prueba crece), pero \(\overline{err}\) típicamente es una estimación mala del error de predicción.

Ejemplo

Vamos a usar simulación para entender estas ideas. Normalmente las muestras de entrenamiento y prueba se extraen del proceso que nos interesa. En este ejemplo simple, usamos simulación usando el siguiente método que se supone no conocemos.

f_real <- function(x){
  ifelse(x < 10, 1000*sqrt(x), 1000*sqrt(10))
}
genera_datos <- function(n = 100){
  x <- runif(n, 0, 25)
  y <- f_real(x) + rnorm(n, 0, 500)
  tibble(x = x, y = y)
}

El método que usaremos por el momento es mínimos cuadrados, que ajusta una recta \(y = a + bx\) a los datos.

library(tidymodels)
modelo_lineal <- linear_reg() %>% 
  set_engine("lm")

Por ejemplo, tenemos la siguiente muestra de entrenamiento:

set.seed(8181)
datos <- genera_datos(30)
datos

## # A tibble: 30 x 2
##        x     y
##    <dbl> <dbl>
##  1  8.41 3568.
##  2  4.37 3299.
##  3 22.7  3620.
##  4 11.2  3794.
##  5 18.6  3070.
##  6  6.81 2655.
##  7  7.10 2632.
##  8  6.53 2509.
##  9 11.0  3431.
## 10  7.42 2834.
## # … with 20 more rows

ggplot(datos, aes(x = x, y = y)) + geom_point()

Ahora podemos usar nuestro algoritmo para construir un predictor, en este caso ajustando por mínimos cuadrados:

mod_1 <- modelo_lineal %>% fit(y ~ x, datos)

calcular_grafica <- function(mod, nombre = ""){
  datos_g <- tibble(x = seq(0, 25, 0.01))
  datos_g <- predict(mod, datos_g) %>% 
    bind_cols(datos_g)
  datos_g %>% mutate(nombre = nombre)
}
datos_g <- calcular_grafica(mod_1)
ggplot(datos, aes(x = x)) +
  geom_point(aes(y = y)) +
  geom_line(data = datos_g, aes(y = .pred), colour = "red")

Ahora tenemos que evaluar este modelo. No podemos usar la muestra de entrenamiento que ya usamos para ajustar la recta. Supongamos entonces que extraemos una muestra grande de prueba:

datos_prueba <- genera_datos(n = 1000)

Y finalmente evaluamos nuestro modelo. Usaremos la raíz de la pérdida cuadrática:

error_1 <- predict(mod_1, datos_prueba) %>% 
  bind_cols(datos_prueba) %>% 
  rmse(truth = y, estimate = .pred)
error_1

## # A tibble: 1 x 3
##   .metric .estimator .estimate
##   <chr>   <chr>          <dbl>
## 1 rmse    standard        722.

Importancia de la tarea supervisada

Esta formulación de la tarea de aprendizaje supervisado ha sido muy productiva (Donoho (2017)), y ha permitido avances grandes en muchos problemas interesantes desde hace unas cuantas décadas. En parte es porque esta formulación es relativamente fácil de implementar para agregar contribuciones de muchas personas. Sitios como Kaggle son implementaciones donde:

• Hay un conjunto de datos disponibles, con los que cualquiera puede construir modelos
• Existen competidores que se inscriben y producen reglas de predicción
• Hay un referee que evalúa las reglas de los concursantes usando datos a los que sólo el referee tiene acceso.
• (En algunos casos) Al final del concurso, los competidores muestran su metodología.

Ejemplo: el concurso de Netflix (2009) siguió este patrón. De este concurso se desarrolló parcialmente el área ahora floreciente de sistemas de recomendación.

1.7 Tres ejemplos de ajustes

¿De qué depende tener buen desempeño en la tarea de aprendizaje supervisado? Comenzamos mostrando algunas formas de construir predicciones en un ejemplo simple, y cómo los evaluaríamos. Nos interesa comenzar contestar las preguntas:

• ¿Por qué son diferentes error de entrenamiento y error de prueba?
• ¿Por qué unos métodos son mejores que otros para un problema dado?
• ¿Por qué los errores de predicción pueden ser altos?
• ¿Qué hacer cuando las predicciones del modelo son malas?

Ejemplo

¿Cuál de los siguientes tres ajustes crees que desempeñe mejor? ¿Cuál crees que tiene el mejor error de entrenamiento? ¿Cuál crees que tiene el mejor error de prueba?

modelo_svm <- svm_poly() %>% 
  set_engine("kernlab") %>% 
  set_mode("regression")
mod_2 <- modelo_svm %>% set_args(cost = 0.1, degree = 3) %>% 
  fit(y ~ x, datos)
mod_3 <- modelo_svm %>% set_args(cost = 100, degree = 8) %>% 
  fit(y ~ x, datos)

datos_1 <- calcular_grafica(mod_1, "modelo 1")
datos_2 <- calcular_grafica(mod_2, "modelo 2")
datos_3 <- calcular_grafica(mod_3, "modelo 3")
datos_g <- bind_rows(datos_1, datos_2, datos_3)
ggplot(datos, aes(x = x)) +
  geom_line(data = datos_g, aes(y = .pred, colour = nombre, group = nombre), size = 1.5) +
    geom_point(aes(y = y)) 

Evaluamos primero error de entrenamiento:

calcular_error <- function(mod_1, datos_prueba){
  error <- predict(mod_1, datos_prueba) %>% 
    bind_cols(datos_prueba) %>% 
    rmse(truth = y, estimate = .pred) 
  error
}

error_tbl <- tibble(modelo = list(mod_1, mod_2, mod_3)) %>% 
  mutate(error_entrena = map_dbl(modelo, 
    ~calcular_error(.x, datos) %>% pull(.estimate)))
error_tbl %>% mutate_if(is.numeric, round)

## # A tibble: 3 x 2
##   modelo   error_entrena
##   <list>           <dbl>
## 1 <fit[+]>           698
## 2 <fit[+]>           535
## 3 <fit[+]>           455

Y ahora agregamos el error de prueba

error_tbl <- error_tbl %>% 
  mutate(error_prueba = map_dbl(modelo, 
    ~calcular_error(.x, datos_prueba) %>% pull(.estimate)))
error_tbl %>% mutate_if(is.numeric, round)

## # A tibble: 3 x 3
##   modelo   error_entrena error_prueba
##   <list>           <dbl>        <dbl>
## 1 <fit[+]>           698          722
## 2 <fit[+]>           535          552
## 3 <fit[+]>           455          714

Ahora explicamos lo que observamos en este ejemplo.

Observaciones

• El “mejor” modelo en entrenamiento es uno que sobreajusta a los datos, pero es el peor con una muestra de prueba. La curva 3 aprende de la componente de ruido del modelo - lo cual realmente no es aprendizaje. Tiene una brecha grande entre entrenamiento y prueba.

• El modelo de la recta no es bueno en entrenamiento ni en prueba. Este modelo no tiene la capacidad para aprender de la señal en los datos.

• El mejor modelo en la muestra de prueba es uno que está entre la recta y la curva 3 en términos de flexibilidad.

• Nuestra intuición para escoger el modelo 2 desde el principio se refleja en que generaliza mejor que los otros, y eso a su vez se refleja en un error de prueba más bajo.

1.8 Aprendizaje y ajuste de curvas

Una manera de entender por qué pasa eso es considerando la situación donde la relación entre \(x\) y \(y\) se puede expresar como

\[y = f(x) + \epsilon\] donde \(\epsilon\) es una término de error aleatorio que tiene valor esperado \(\textrm{E}(\epsilon | x)=0\) (su media no depende de los valores de las entradas).

• \(f\) expresa la relación sistemática que hay entre \(y\) y \(x\): para cada valor posible de \(x\), la contribución de \(x\) a \(y\) es \(f(x)\). Típicamente es una función complicada de \(x\).
• Pero \(x\) no determina a \(y\), agregamos una error aleatorio \(\epsilon\), con media cero (si la media no es cero podemos agregar una constante a \(f\)).
• \(\epsilon\) representa, por ejemplo, el efecto de variables que no hemos medido o procesos aleatorios que determinan la respuesta.

En este caso, si consideramos la diferencia entre la predicción y el valor verdadero para un caso particular, podemos escribir:

\[ y-\hat{y} = f(x) + \epsilon - \hat{f}(x)= (f(x) - \hat{f}(x)) + \epsilon,\] donde vemos que hay dos componentes que pueden hacer grande a \(y-\hat{y}\): - La diferencia \(f(x) - \hat{f}(x)\) está asociada a error reducible, pues depende de qué tan bien estimemos \(f(X)\) con \(\hat{f}(x)\) - El error aleatorio \(\epsilon\), asociado a error irreducible.

Queremos que nuestro modelo ajustado \(\hat{f}\) esté cerca de \(f\), pues no podemos hacer nada acerca de \(\epsilon\). Hay dos razones por las \(f\) puede estar lejos de \(\hat{f}\):

• \(\hat{f}(x)\) está consistemente lejos de \(f(x)\) para algunas \(x\) porque no puede capturar patrones que están en los datos (sesgo)
• \(\hat{f}(x)\) varía mucho con la muestra de entrenamiento, de manera que es probable que para nuestra muestra caiga lejos de \(f(x)\) (varianza)

Una manera de cuantificar esto es mediante la descomposición varianza-sesgo. Con algunos cálculos simples, podemos demostrar que el error de predicción (con error cuadrático) se descompone en (con \(x\) fija):

\[E \left [(y-\hat{f}(x))^2 \right ] = \left[ E(\hat{f}(x)) - f(x) \right]^2 + Var(\hat{f}(x)) + Var(\epsilon)\]

donde el valor esperado es sobre el conjunto de entrenamiento \({\mathcal L}\) y \(\epsilon\) (es decir, promediando sobre muestras de entrenamiento posibles).

• El primer término le llamamos sesgo del predictor (si está consistentemente lejos de \(f(x)\))
• El segundo término es la varianza del predictor (qué tan sensible es a la muestra de entrenamiento)
• Al tercer término le llamamos error irreducible.

Este resultado explica lo que observamos en nuestro ejemplo de simulación. En análisis predictivo, buscamos encontrar el mejor balance de estos dos tipos de errores (sesgo y varianza).

1.9 Balance de complejidad y rigidez

Como vimos en el ejemplo de arriba, el error de entrenamiento no es un buen indicador del desempeño futuro de nuestras predicciones. Para evaluar este desempeño, necesitamos una muestra de prueba independiente de la muestra que usamos para aprender o para entrenar el modelo.

Intuitivamente esto tiene sentido: en el proceso de aprendizaje tenemos disponibles las etiquetas (sabemos las respuestas), de modo que puede suceder que el algoritmo memorice la asociación de qué etiquetas \(y^{(i)}\) van con cada conjunto de entradas \(x^{(i)}\). Esto se dice de varias maneras, por ejemplo:

• El modelo sobreajusta a los datos: esto quiere decir que por ajustar aspectos de los datos de entrenamiento demasiado fuertemente, el algoritmo parece replicar de cerca los datos de entrenamiento pero se desempeña mal en la predicción.

• El modelo aprende del ruido: nuestro proceso de aprendizaje captura aspectos irrelevantes de los datos, que nuevos datos no van a compartir.

• El modelo no tiene capacidad de generalización, porque captura aspectos que solo están presentes en nuestra muestra de entrenamiento.

• El modelo tiene varianza alta, porque cambia mucho dependiendo de la muestra de entrenamiento.

• El modelo es demasiado complejo o flexible y fácilmente se adapta a cualquier conjunto de datos, tanto señal como ruido.

En el ejemplo de arriba, también vimos que algunos modelos pueden tener desempeño malo porque no tienen la capacidad de aprender de patrones reales y generales en los datos (la recta en el ejemplo anterior). Podemos decir esto de varias maneras:

• El modelo subajusta a los datos: no tienen la capacidad de ajustar aspectos de los datos de entrenamiento que son relaciones reales entre las variables.

• El modelo ignora señal en los datos: el algoritmo no captura aspectos relevantes de los datos, que comparten con nuevos datos y pueden utilizarse para hacer predicciones.

• El modelo no tiene capacidad de aprendizaje, pues no puede capturar aspectos que son generales para el fenómeno de interés.

• El modelo tiene sesgo alto, porque no puede ajustar patrones generalizables en los datos.

• El modelo es demasiado rígido, y no puede adaptarse ni siquiera a patrones fuertes y claros en los datos.

Logramos buenas predicciones cuando refinamos nuestros modelos o algoritmos para lograr aprender de la señal e ignorar el ruido, que no ayuda en la predicción, y lograr reducir el error de predicción lo más posible con los datos disponibles. Esto requiere buscar el nivel adecuado de complejidad en los modelos o algoritmos para los datos que tenemos.

Para construir buenos predictores, requerimos que:

• El algoritmo tenga la flexibilidad necesaria para capturar patrones generales y fuertes en los datos.
• El algoritmo tenga la rigidez necesaria para tener robustez a patrones de ruido o particularidades no repetibles de nuestra muestra de entrenamiento.
• El algoritmo es apropiado para el problema: dependiendo de estructura conocida que incluyamos en el modelo, el balance de flexibilidad y rigidez es diferente.
• Saber intuitivamente cuál es el grado adecuado de complejidad para un problema dado es difícil. Para decidirlo, evaluamos el desempeño de nuestros métodos usando una muestra de prueba. El nivel adecuado de complejidad se traduce en menos error de predicción.

1.10 ¿Cómo estimar f?

Ahora mostramos otro aspecto característico del aprendizaje supervisado. En primer lugar, el método general más usual para encontrar \(\hat{f}\) es hacer lo siguiente:

• Consideramos una familia de funciones \(h\) candidatas para aproximar \(f\)
• Calculamos el error de entrenamiento de cada posible \(h\), y encontramos la \(h\) que minimiza el error de entrenamiento (la que más se ajusta a los datos de entrenamiento). Tomamos \(\hat{f} = h\). Si usamos la pérdida cuadrática,

\[\hat{f} = \min_h \frac{1}{N}\sum_{i=1}^N (y^{(i)} - h(x^{(i)}))^2.\] - Evaluar el error de predicción del modelo que seleccionamos (queremos que sea bajo):

\[\hat{Err} = \frac{1}{m}\sum_{j=1}^m (\mathbf{y}^{(j)} - \hat{f}(\mathbf{x}^{(j)}))^2\]

De modo que el proceso es un problema de minimización. Lo que hace interesante nuestro caso es que realmente no queremos minimizar el error de entrenamiento. Queremos minimizar el error de prueba. O sea que minimizamos una cantidad que realmente no nos interesa (error de entrenamiento) con la esperanza de minimizar la cantidad que nos interesa (error de predicción).

Como es de esperarse, este esquema simple no funciona muy bien sin afinar algunos aspectos. Para que la solución anterior sea razonable o buena:

• Tenemos que ser cuidadosos y poder regular la elección de la familia inicial de funciones (rectas? curvas muy flexibles? etc.). Buscamos familias que tengan la estructura adecuada para cada problema.
• A veces tenemos que modificar el objetivo del problema de minimización para que nos obligue encontrar un balance adecuado de complejidad y error de predicción bajo. Por ejemplo, penalizar el objetivo de modelos que son poco creíbles o demasiado complicados.
• Perturbar la muestra de entrenamiento de distintas maneras para evitar que un algoritmo aprenda información irrelevante.

La mayor parte del curso se concentra en considerar qué familias o modelos podemos utilizar en distintos casos, qué modificaciones de la función objetivo pueden hacerse para mejorar el proceso de entrenamiento, y qué perturbaciones de los datos pueden considerarse para mejorar el desempeño predictivo de nuestros modelos.

1.11 Qué cosas no veremos en este curso

En este curso nos concentraremos en la construcción, evaluación y mejora de modelos predictivos. Para que estas ideas funcionen en problemas reales, hay más aspectos a considerar que no discutiremos con detalle (y muchas veces son considerablemente más difíciles de la teoría y los algoritmos):

• La aplicación de aprendizaje de máquina requiere, en primer lugar, de que los datos correctos sean identificados y capturados. Esto en muchos casos requiere esfuerzos concentrados en esta dirección y típicamente no sucede sino hasta cuando comenzamos el trabajo de construir modelos predictivos (o al menos el trabajo de construir conjuntos de reglas).

• Para entender exactamente cuál es el problema que queremos resolver se requiere trabajo analítico considerable, y también trabajo en entender aspectos del negocio/área donde nos interesa usar aprendizaje máquina. Muchas veces es fácil resolver un problema muy preciso, que tenemos a la mano, pero que más adelante nos damos cuenta de que no es útil.

• Estos dos puntos incluyen indentificar las métricas que queremos mejorar, lo cual no siempre se claro. Optimizar métricas incorrectas es poco útil en el mejor de los casos, y en los peores pueden causar daños. Evitar esto requiere monitoreo constante de varios aspectos del funcionamiento de nuestros modelos y sus consecuencias.

• ¿Cómo poner en producción modelos y mantenerlos? Un flujo apropiado de trabajo, y de entrenamiento continuo puede ser la diferencia entre entre un modelo exitoso o uno que se vuelve fuente de dificultades y confusión.

1.12 Resumen

• Aprendizaje de máquina: algoritmos que aprenden de los datos para predecir cantidades numéricas, o clasificar (aprendizaje supervisado), o para encontrar estructura en los datos (aprendizaje no supervisado).

• En aprendizaje supervisado, el esquema general es:

  • Un algoritmo aprende de una muestra de entrenamiento \({\mathcal L}\), que es generada por el proceso generador de datos que nos interesa. Eso quiere decir que produce una función \(\hat{f}\) (a partir de \({\mathcal L}\)) que nos sirve para hacer predicciones \(x \to \hat{f}(x)\) de \(y\)
  • El error de predicción del algoritmo es \(Err\), que mide en promedio qué tan lejos están las predicciones de valores reales.
  • Para estimar esta cantidad usamos una muestra de prueba \({\mathcal T}\), que es independiente de \({\mathcal L}\).
  • Esta es porque nos interesa el desempeño futuro de \(\hat{f}\) para nuevos casos que el algoritmo no ha visto (esto es aprender).

• El error en la muestra de entrenamiento no necesariamente es buen indicador del desempeño futuro de nuestro algoritmo.

• Para obtener las mejores predicciones posibles, es necesario que el algoritmo sea capaz de capturar patrones en los datos, pero no tanto que tienda a absorber ruido en la estimación - es un balance de complejidad y rigidez. En términos estadísticos, se trata de un balance de varianza y sesgo.