Clase 2 Modelos lineales y descenso en gradiente

Consideramos un problema de regresión con entradas \(x=(x_1,x_2,\ldots, Xxp)\) y respuesta \(y\). Buscamos una familia de funciones \(\mathcal F\) apropiada, de forma que dados unos datos de entrenamiento \(\mathcal L\) escojamos una función \(\hat{f}\in \mathcal F\) para hacer predicciones. Nos gustaría que el error predictivo \(Err(\hat{f})\) sea bajo.

2.1 Modelos lineales

Una de las maneras más simples que podemos intentar para predecir \(y\) en función de las \(x_j\)´s es mediante una suma ponderada de los valores de las \(x_j's\), usando una función de la forma

\[f_\beta (x) = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \cdots + \beta_p x_p,\] En este caso, escoger una función particular de esta familia, dada una muestra de entrenamiento \({\mathcal L}\), consiste en encontrar encontrar valores apropiados de las \(\beta\)’s, para construir un predictor:

\[\hat{f}(x) = \hat{\beta}_0 + \hat{\beta}_1 x_1 + \hat{\beta}_2 x_2 \cdots + \hat{\beta} x_p\] y usaremos esta función \(\hat{f}\) para hacer predicciones \(\hat{y} =\hat{f}(x)\).

Ejemplos

Queremos predecir las ventas futuras anuales \(y\) de una tienda que se va a construir en un lugar dado. Las variables que describen el lugar son \(x_1 = trafico\_peatones\), \(x_2=trafico\_coches\). En una aproximación simple, podemos suponer que la tienda va a capturar una fracción de esos tráficos que se van a convertir en ventas. Quisieramos predecir con una función de la forma \[f_\beta (peatones, coches) = \beta_0 + \beta_1\, peatones + \beta_2\, coches.\] Por ejemplo, después de un análisis estimamos que

\(\hat{\beta}_0 = 1000000\) (ventas base, si observamos tráficos igual a 0: es lo que va a atraer la tienda)
\(\hat{\beta}_1 = (200)*0.02 = 4\) (capturamos 2% del tráfico peatonal, y cada capturado gasta 200 pesos)
\(\hat{\beta}_2 = (300)*0.01 =3\) (capturamos 1% del tráfico de autos, y cada capturado gasta 300 pesos) Entonces haríamos predicciones con \[\hat{f}(peatones, coches) = 1000000 + 4\,peatones + 3\, coches.\] El modelo lineal es más flexible de lo que parece en una primera aproximación, porque tenemos libertad para construir las variables de entrada a partir de nuestros datos. Por ejemplo, si tenemos una tercera variable \(estacionamiento\) que vale 1 si hay un estacionamiento cerca o 0 si no lo hay, podríamos definir las variables
\(x_1= peatones\)
\(x_2 = coches\)
\(x_3 = estacionamiento\)
\(x_4 = coches*estacionamiento\)

Donde la idea de agregar \(x_4\) es que si hay estacionamiento entonces vamos a capturar una fracción adicional del trafico de coches, y la idea de \(x_3\) es que la tienda atraerá más nuevas visitas si hay un estacionamiento cerca. Buscamos ahora modelos de la forma \[f_\beta(x_1,x_2,x_3,x_4) = \beta_0 + \beta_1x_1 + \beta_2 x_2 + \beta_3 x_3 +\beta_4 x_4\] y podríamos obtener después de nuestra análisis las estimaciones - \(\hat{\beta}_0 = 800000\) (ventas base) - \(\hat{\beta}_1 = 4\) - \(\hat{\beta}_2 = (300)*0.005 = 1.5\) - \(\hat{\beta}_3 = 400000\) (ingreso adicional si hay estacionamiento por nuevo tráfico) - \(\hat{\beta}_4 = (300)*0.02 = 6\) (ingreso adicional por tráfico de coches si hay estacionamiento)

y entonces haríamos predicciones con el modelo \[\hat{f} (x_1,x_2,x_3,x_4) = 800000 + 4\, x_1 + 1.5 \,x_2 + 400000\, x_3 +6\, x_4\]

2.2 Aprendizaje de coeficientes (ajuste)

En el ejemplo anterior, los coeficientes fueron calculados (o estimados) usando experiencia, reglas, argumentos teóricos, o quizá otras fuentes de datos (como estudios o encuestas, conteos, etc.)

Ahora quisiéramos construir un algoritmo para aprender estos coeficientes del modelo \[f_\beta (X_1) = \beta_0 + \beta_1 X_1 + \cdots \beta_p X_p\] a partir de una muestra de entrenamiento de datos históricos de tiendas que hemos abierto antes: \[{\mathcal L}=\{ (x^{(1)},y^{(1)}),(x^{(2)},y^{(2)}), \ldots, (x^{(N)}, y^{(N)}) \}\] El criterio de ajuste (algoritmo de aprendizaje) más usual para regresión lineal es el de mínimos cuadrados.

Construimos las predicciones (ajustados) para la muestra de entrenamiento: \[\hat{y}^{(i)} = f_\beta (x^{(i)}) = \beta_0 + \beta_1 x_1^{(i)}+ \cdots + \beta_p x_p^{(i)}\]

Y consideramos las diferencias de los ajustados con los valores observados:

\[e^{(i)} = y^{(i)} - f_\beta (x^{(i)})\]

La idea entonces es minimizar la suma de los residuales al cuadrado, para intentar que la función ajustada pase lo más cercana a los puntos de entrenamiento que sea posible. La función de pérdida que utilizamos más frecuentemente es la pérdida cuadrática, dada por:

\[L(\beta) = ECM(\beta) = \frac{1}{N}\sum_{i=1}^N (y^{(i)} - f_\beta(x^{(i)}))^2\] (ECM es el error cuadrático medio).

Mínimos cuadrados para regresión lineal Buscamos encontrar: \[\hat{\beta} = \mathrm{arg\,min}_{\beta} L(\beta) = \mathrm{arg\,min}_{\beta}\frac{1}{N}\sum_{i=1}^N (y^{(i)} - f_\beta(x^{(i)}))^2\] donde \[f_\beta (x^{(i)}) = \beta_0 + \beta_1 x_1^{(i)}+ \cdots + \beta_p x_p^{(i)}\]

Observación: Como discutimos al final de las sección anterior, minimizar directamente el error de entrenamiento para encontrar los coeficientes puede resultar en en un modelo sobreajustado/con varianza alta/ruidoso. Hay tres grandes estrategias para mitigar este problema: restringir o estructurar la familia de funciones, penalizar la función objetivo o perturbar la muestra de entrenamiento. El método mas común es cambiar la función objetivo, que discutiremos más adelante en la sección de regularización.

Ejemplo

Consideramos el problema de predecir el precio de venta de una casa en términos de sus características. Para esto usamos datos de este concurso de Kaggle.

library(tidyverse)
casas <- read_csv("../datos/houseprices/house-prices.csv")
casas %>% names

##  [1] "Id"            "MSSubClass"    "MSZoning"      "LotFrontage"  
##  [5] "LotArea"       "Street"        "Alley"         "LotShape"     
##  [9] "LandContour"   "Utilities"     "LotConfig"     "LandSlope"    
## [13] "Neighborhood"  "Condition1"    "Condition2"    "BldgType"     
## [17] "HouseStyle"    "OverallQual"   "OverallCond"   "YearBuilt"    
## [21] "YearRemodAdd"  "RoofStyle"     "RoofMatl"      "Exterior1st"  
## [25] "Exterior2nd"   "MasVnrType"    "MasVnrArea"    "ExterQual"    
## [29] "ExterCond"     "Foundation"    "BsmtQual"      "BsmtCond"     
## [33] "BsmtExposure"  "BsmtFinType1"  "BsmtFinSF1"    "BsmtFinType2" 
## [37] "BsmtFinSF2"    "BsmtUnfSF"     "TotalBsmtSF"   "Heating"      
## [41] "HeatingQC"     "CentralAir"    "Electrical"    "1stFlrSF"     
## [45] "2ndFlrSF"      "LowQualFinSF"  "GrLivArea"     "BsmtFullBath" 
## [49] "BsmtHalfBath"  "FullBath"      "HalfBath"      "BedroomAbvGr" 
## [53] "KitchenAbvGr"  "KitchenQual"   "TotRmsAbvGrd"  "Functional"   
## [57] "Fireplaces"    "FireplaceQu"   "GarageType"    "GarageYrBlt"  
## [61] "GarageFinish"  "GarageCars"    "GarageArea"    "GarageQual"   
## [65] "GarageCond"    "PavedDrive"    "WoodDeckSF"    "OpenPorchSF"  
## [69] "EnclosedPorch" "3SsnPorch"     "ScreenPorch"   "PoolArea"     
## [73] "PoolQC"        "Fence"         "MiscFeature"   "MiscVal"      
## [77] "MoSold"        "YrSold"        "SaleType"      "SaleCondition"
## [81] "SalePrice"

¿Cuáles deberían ser las variables más importantes? Debemos considerar al menos, el tamaño de las casas, la calidad de sus terminados, su ubicación, y tipo de casa (dos pisos, un piso, etc.). Vamos a comenzar consierando tamaño, calidad y tipo de casa. Un modelo que no tiene mucho sentido empezar ajustando es

\[Precio = \beta_0 + \beta_1 Calidad + \beta_2 Tamaño + \beta_3 Pisos,\]

porque esto implicaría que el precio por metro cuadrado de las casas es constante, y la calidad de las casas solo aporta una cantidad fija a su precio total. Una estrategia que podemos considerar es el modelo:

\[Precio = \left( \beta_0 + \beta_1 \,Calidad + \beta_2 \,Pisos\right) \, Tamaño\] Es decir, el precio por metro cuadrado varía con la calidad y el número de pisos. Podemos modelar entonces, en lugar del Precio,

\[Precio_{m^2} = \beta_0 + \beta_1 \, Calidad + \beta_2 \, Pisos,\]

y este es un modelo lineal. Para hacer predicciones del Precio, después multiplicamos la predicción del precio por metros cuadrados por Tamaño.

En primer lugar, es necesario separar los datos en al menos dos partes: una parte para entrenar y otra para evaluar y estimar el error de predicción.

library(tidymodels)

## Warning: package 'parsnip' was built under R version 4.0.3

casas_split <- initial_split(casas, prop = 0.7)
train <- training(casas_split)
test <- testing(casas_split)

Y tendremos que hacer limpieza de datos. Esto normalmente se hace con la muestra de entrenamiento, y después aplicamos los mismos procesos a la muestra de prueba. En nuestro caso, después de alguna exploración de los datos de entrenamiento notamos en primer lugar que hay ciertas ventas anormales:

train %>% group_by(SaleCondition) %>% 
  count()

## # A tibble: 6 x 2
## # Groups:   SaleCondition [6]
##   SaleCondition     n
##   <chr>         <int>
## 1 Abnorml          67
## 2 AdjLand           4
## 3 Alloca            9
## 4 Family           15
## 5 Normal          837
## 6 Partial          90

Esta es una variable que no podemos utilizar, pues solo se sabe después de la venta. Discute razones por las que incluir esta variable en nuestras predicciones puede ser mala idea.

Podríamos usar el siguiente código para explorar:

calc_cuantiles <- function(x, probs = c(0, 0.25, 0.5, 0.75, 1.0)){
  cuantiles <- quantile(x, probs = probs)
  tibble(f = names(cuantiles), cuantil = cuantiles) %>% list
}
limpiar_casas <- function(datos){
  datos_limpios <- datos %>% 
    mutate(tiene_piso_2 = as.numeric(`2ndFlrSF` > 0),
           precio_miles = SalePrice / 1000, 
           habitable_m2 = (GrLivArea * 0.092903),
           precio_m2_miles = precio_miles / habitable_m2,
           calidad = OverallQual - 6, 
           habitaciones = BedroomAbvGr) %>%
    filter(SaleCondition %in% c("Normal", "AdjLand")) %>% 
    select(Id, tiene_piso_2:habitaciones) 
  datos_limpios
} 
datos_exp <- limpiar_casas(train)
cuantiles_tbl <- datos_exp %>% 
  summarise(across(where(is.numeric), calc_cuantiles)) %>% 
  pivot_longer(cols = everything(), names_to = "variable", values_to = "datos") %>% 
  unnest(cols = datos) 
cuantiles_tbl %>% mutate(cuantil = round(cuantil)) %>% 
  pivot_wider(names_from = f, values_from = cuantil)

## # A tibble: 7 x 6
##   variable         `0%` `25%` `50%` `75%` `100%`
##   <chr>           <dbl> <dbl> <dbl> <dbl>  <dbl>
## 1 Id                  1   354   737  1111   1460
## 2 tiene_piso_2        0     0     0     1      1
## 3 precio_miles       39   130   160   205    755
## 4 habitable_m2       31   102   134   164    401
## 5 precio_m2_miles     0     1     1     1      2
## 6 calidad            -5    -1     0     1      4
## 7 habitaciones        0     2     3     3      6

graf_ent <- ggplot(datos_exp, aes(x = calidad, y = precio_m2_miles)) + 
    geom_jitter(size=1, alpha = 0.5, width = 0.3, height = 0) + 
    facet_wrap(~tiene_piso_2) 
graf_ent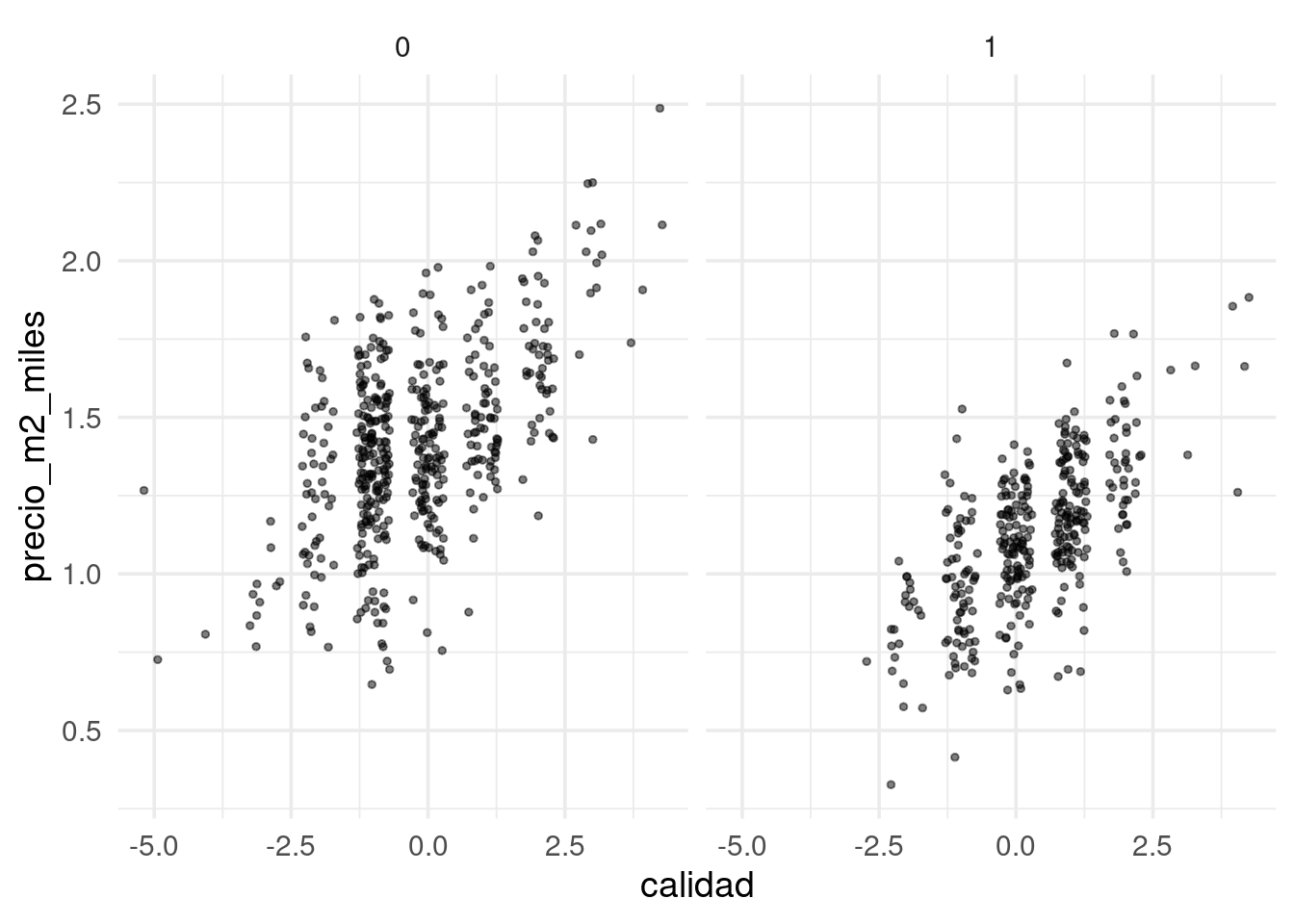

Una vez que estamos satisfechos por el momento con la exploración, podemos crear nuestro flujo de procesamiento:

train_tbl <- limpiar_casas(train)
test_tbl <- limpiar_casas(test)
# usamos recipes para este ejemplo, no necesitas usarlo
casas_receta <- recipe(precio_m2_miles ~ ., train_tbl) %>%
  update_role(Id, precio_miles, habitable_m2, habitaciones, new_role = "none") 
casas_receta %>% summary()

## # A tibble: 7 x 4
##   variable        type    role      source  
##   <chr>           <chr>   <chr>     <chr>   
## 1 Id              numeric none      original
## 2 tiene_piso_2    numeric predictor original
## 3 precio_miles    numeric none      original
## 4 habitable_m2    numeric none      original
## 5 calidad         numeric predictor original
## 6 habitaciones    numeric none      original
## 7 precio_m2_miles numeric outcome   original

modelo_lineal <- linear_reg() %>%
  set_engine("lm")
casas_flujo <- workflow() %>%
  add_recipe(casas_receta) %>% 
  add_model(modelo_lineal)

Ajustamos usando mínimos cuadrados (según el engine lm):

ajuste <- fit(casas_flujo, train_tbl)
ajuste

## ══ Workflow [trained] ════════════════════════════════════════════════════════════════════════════════
## Preprocessor: Recipe
## Model: linear_reg()
## 
## ── Preprocessor ──────────────────────────────────────────────────────────────────────────────────────
## 0 Recipe Steps
## 
## ── Model ─────────────────────────────────────────────────────────────────────────────────────────────
## 
## Call:
## stats::lm(formula = ..y ~ ., data = data)
## 
## Coefficients:
##  (Intercept)  tiene_piso_2       calidad  
##       1.4424       -0.3582        0.1221

Ahora podemos comparar ajustados con observados:

casas_ajustados <- predict(ajuste, train_tbl) %>% 
  bind_cols(train_tbl)
casas_ajustados

## # A tibble: 841 x 8
##    .pred    Id tiene_piso_2 precio_miles habitable_m2 precio_m2_miles calidad
##    <dbl> <dbl>        <dbl>        <dbl>        <dbl>           <dbl>   <dbl>
##  1 1.21      1            1         208.        159.             1.31       1
##  2 1.44      2            0         182.        117.             1.55       0
##  3 0.962     6            1         143         127.             1.13      -1
##  4 1.69      7            0         307         157.             1.95       2
##  5 1.21      8            1         200         194.             1.03       1
##  6 1.32     10            0         118         100.             1.18      -1
##  7 1.32     13            0         144          84.7            1.70      -1
##  8 1.44     15            0         157         116.             1.35       0
##  9 1.56     16            0         132          79.3            1.66       1
## 10 1.32     19            0         159         103.             1.54      -1
## # … with 831 more rows, and 1 more variable: habitaciones <dbl>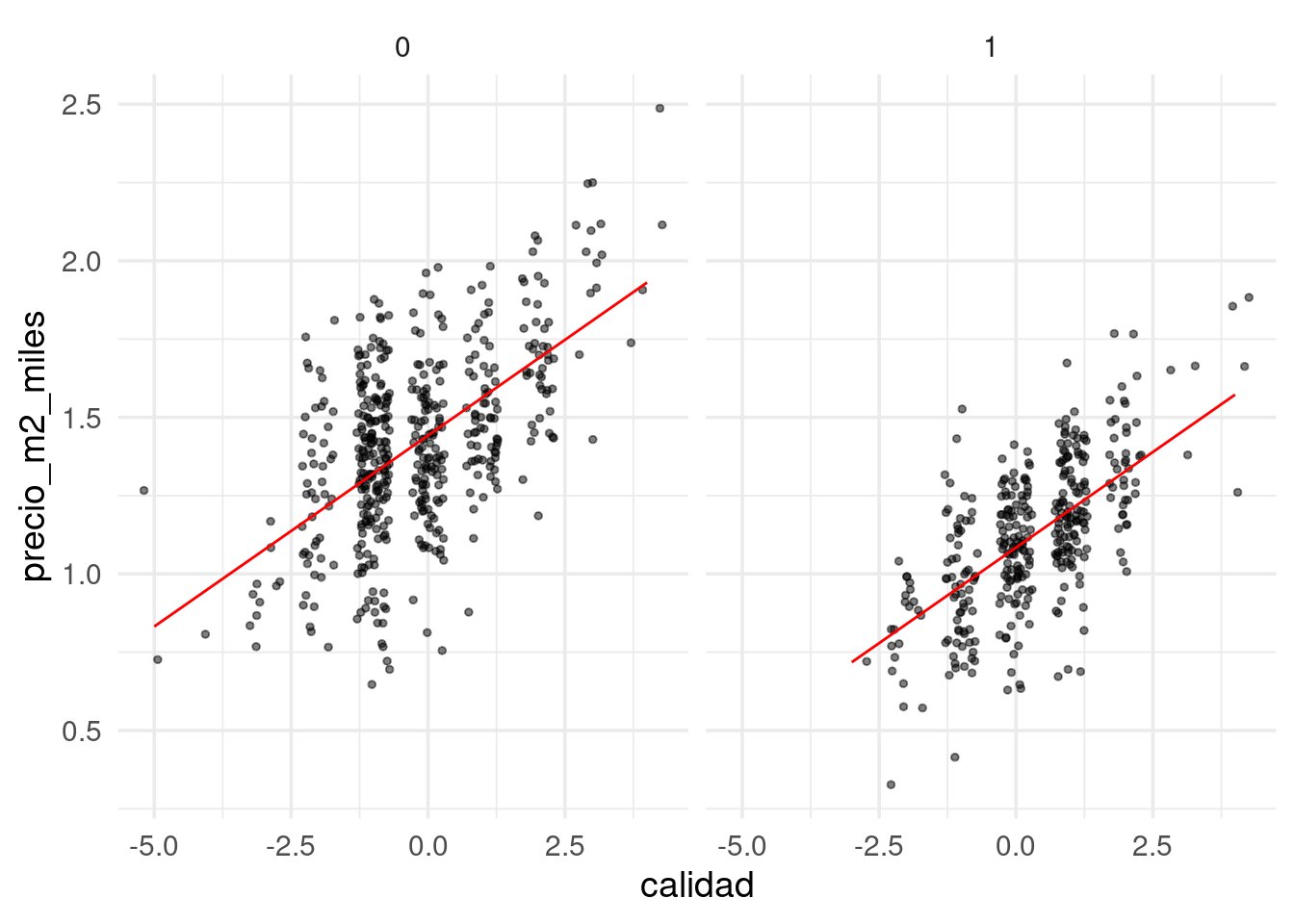

graf_ent + geom_line(data = casas_ajustados, aes(y = .pred), colour = "red")

Y evaluamos nuestras predicciones con el conjunto de prueba:

casas_pred <- predict(ajuste, test_tbl) %>% 
  bind_cols(test_tbl %>% select(precio_m2_miles))
metricas <- metric_set(rmse, mae, mape)
casas_pred %>% 
  metricas(precio_m2_miles, .pred) %>% 
  mutate(across(where(is.numeric), round, 2))

## # A tibble: 3 x 3
##   .metric .estimator .estimate
##   <chr>   <chr>          <dbl>
## 1 rmse    standard        0.21
## 2 mae     standard        0.17
## 3 mape    standard       15.0

Pregunta: ¿cómo se hizo el ajuste en este caso (el engine que usamos fue lm)? ¿Qué algoritmo se usó para minimizar la suma de cuadrados?

2.3 Aprendizaje de parámetros para regresión lineal

Ahora veremos cómo resolver el problema de minimización para ajustar el modelo de regresión lineal con error cuadrático. Hay varias maneras de hacer esto:

En el enfoque tradicional, se usan soluciones analíticas del problema de minimización y técnicas de álgebra lineal (por ejemplo, lm en R). Este método es efectivo para problemas chicos y medianos, utilizan álgebra lineal avanzada y son numéricamente probados. Estas técnicas se escalan en parte a problemas grandes, pero no es muy simple hacerlo.
Es posible utilizar algoritmos de optimización estándar. Hay una variedad grande de ellos, algunos muy sofisticados y poderosos, pero en muchos problemas grandes no necesariamente escalan apropiadamente.
En términos de escalamiento y simplicidad, el método de descenso en gradiente y sus variantes es muy efectivo para escalar a datos grandes y modelos más complejos (por ejemplo redes neuronales).

Notamos que el problema de minimización para regresión no es particularmente difícil:

Se puede demostrar que la función objectivo es convexa.
Sin embargo, en algunos casos puede ser que la función objetivo tenga regiones muy planas, lo cual hace difícil la optimización para la mayoría de los métodos. En la siguiente sección veremos por qué puede pasar esto y como mejorar este problema.

2.4 Descenso en gradiente para regresión lineal

Aunque el problema de mínimos cuadrados se puede resolver analíticamente, o usando un optimizador avanzado de R, proponemos un método numérico básico que es efectivo y puede escalarse a problemas grandes de manera relativamente simple: descenso en gradiente, o descenso máximo.

Intro a descenso en gradiente

Supongamos que una función \(h(x)\) es convexa y tiene un mínimo. La idea de descenso en gradiente es comenzar con un candidato inicial \(z_0\) y calcular la derivada en \(z^{(0)}\). Si \(h'(z^{(0)})>0\), la función es creciente en \(z^{(0)}\) y nos movemos ligeramente a la izquierda para obtener un nuevo candidato \(z^{(1)}\). si \(h'(z^{(0)})<0\), la función es decreciente en \(z^{(0)}\) y nos movemos ligeramente a la derecha para obtener un nuevo candidato \(z^{(1)}\). Iteramos este proceso hasta que la derivada es cercana a cero (estamos cerca del óptimo).

Si \(\eta>0\) es una cantidad chica, podemos escribir

\[z^{(1)} = z^{(0)} - \eta \,h'(z^{(0)}).\]

Nótese que cuando la derivada tiene magnitud alta, el movimiento de \(z^{(0)}\) a \(z^{(1)}\) es más grande, y siempre nos movemos una fracción de la derivada. En general hacemos \[z^{(j+1)} = z^{(j)} - \eta\,h'(z^{(j)})\] para obtener una sucesión \(z^{(0)},z^{(1)},\ldots\). Esperamos a que \(z^{(j)}\) converja para terminar la iteración.

Ejemplo

Si tenemos

h <- function(x) x^2 + (x - 2)^2 - log(x^2 + 1)

Calculamos (a mano):

h_deriv <- function(x) 2 * x + 2 * (x - 2) - 2*x/(x^2 + 1)

Ahora iteramos con \(\eta = 0.4\) y valor inicial \(z_0=5\)

z_0 <- 5
eta <- 0.4
descenso <- function(n, z_0, eta, h_deriv){
  z <- matrix(0,n, length(z_0))
  z[1, ] <- z_0
  for(i in 1:(n-1)){
    # paso de descenso
    z[i+1, ] <- z[i, ] - eta * h_deriv(z[i, ])
  }
  z
}
z <- descenso(20, z_0, eta, h_deriv)
z

##             [,1]
##  [1,]  5.0000000
##  [2,] -1.2461538
##  [3,]  1.9571861
##  [4,]  0.7498212
##  [5,]  1.5340816
##  [6,]  1.0455267
##  [7,]  1.3722879
##  [8,]  1.1573987
##  [9,]  1.3013251
## [10,]  1.2057209
## [11,]  1.2696685
## [12,]  1.2270627
## [13,]  1.2555319
## [14,]  1.2365431
## [15,]  1.2492245
## [16,]  1.2407623
## [17,]  1.2464122
## [18,]  1.2426413
## [19,]  1.2451587
## [20,]  1.2434784

Y vemos que estamos cerca de la convergencia. Podemos graficar:

dat_iteraciones <- tibble(iteracion = 1:nrow(z), 
                              x = z[, 1], y = h(z[, 1]))

library(gganimate)
curva <- ggplot(tibble(x = seq(-4, 5, 0.1)), aes(x = x)) + stat_function(fun = h) +
     xlim(c(-4, 5))
descenso_g <- curva +
    geom_point(data = dat_iteraciones, aes(x = x, y = y), col = "red", size = 3) +
    transition_time(iteracion) + 
    theme_minimal(base_size = 20)
animate(descenso_g)

Selección de tamaño de paso \(\eta\)

Buscamos un \(\eta\) apropiado para cada problema:

Si hacemos \(\eta\) muy chico, el algoritmo puede tardar mucho en converger.
Si hacemos \(\eta\) demasiado grande, el algoritmo puede divergir.

z_eta_chico <- descenso(20, 5, 0.01, h_deriv)
z_eta_grande <- descenso(20, 1.8, 0.6, h_deriv)
dat_chico <- tibble(iteracion = 1:nrow(z), x = z_eta_chico[, 1], y = h(z_eta_chico[, 1]), tipo = "η = 0.01")
dat_grande <- tibble(iteracion = 1:nrow(z), x = z_eta_grande[, 1], y = h(z_eta_grande[, 1]), tipo = "η = 0.6")
dat_iteraciones$tipo <- "η = 0.03"
dat <- bind_rows(dat_chico, dat_grande, dat_iteraciones)

library(gganimate)
curva <- ggplot(tibble(x = seq(-4, 5, 0.1)), aes(x = x)) + stat_function(fun = h, colour = "gray") +
     xlim(c(-4, 5))
descenso_3 <- curva +
    geom_point(data = dat, aes(x = x, y = y), col = "red", size = 3) +
    facet_wrap(~tipo, nrow = 1) + ylim(c(0, 50)) +
    transition_time(iteracion) +
    labs(title = "Iteración {frame_time}") + 
    theme_minimal(base_size = 20)
animate(descenso_3, width = 1000, height = 300)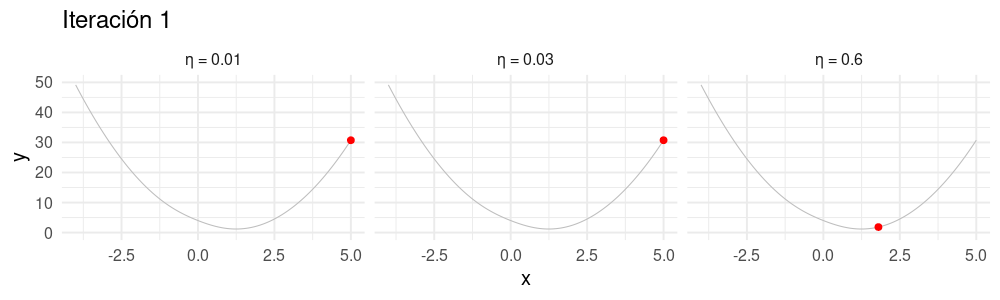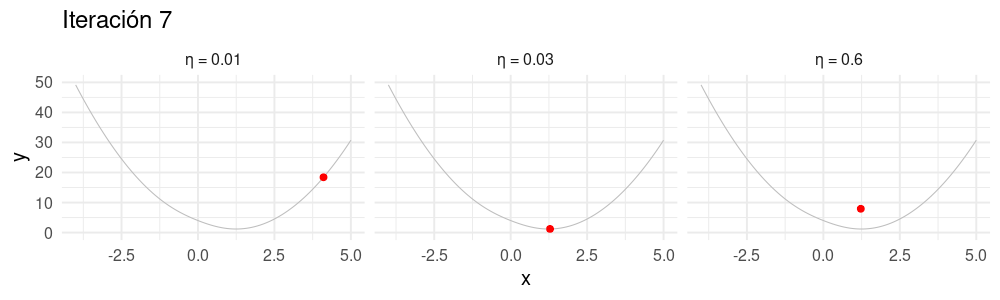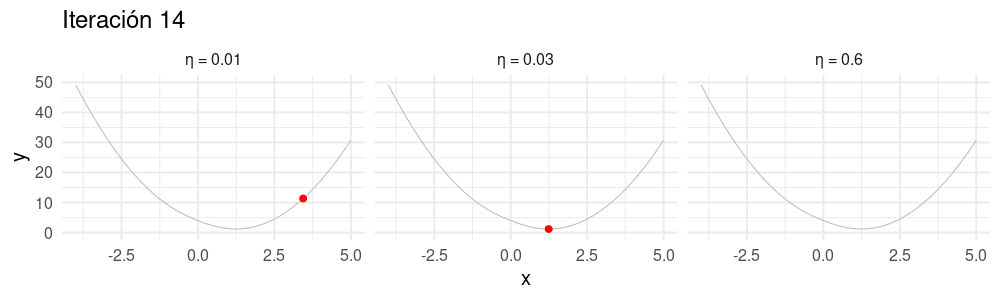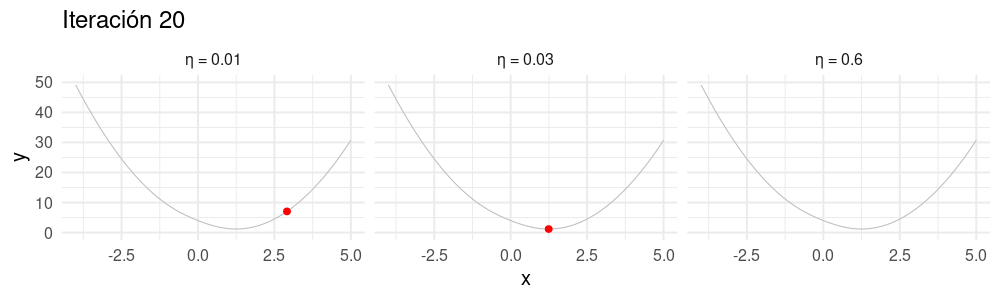

Es necesario ajustar el tamaño de paso para cada problema particular. Si la convergencia es muy lenta, podemos incrementarlo. Si las iteraciones divergen, podemos disminuirlo

Funciones de varias variables

Si ahora \(h(z)\) es una función de \(p\) variables, podemos intentar la misma idea usando el gradiente, que está definido por:

\[\nabla h(z) = \left( \frac{\partial h}{\partial z_1}, \frac{\partial h}{\partial z_2}, \ldots, \frac{\partial h}{\partial z_p} \right)^t,\] es decir, es el vector columna con las derivadas parciales de \(h\).

Por cálculo sabemos que el gradiente apunta en la dirección de máximo crecimiento local, asi que el paso de iteración, dado un valor inicial \(z_0\) y un tamaño de paso \(\eta >0\) es

\[z^{(i+1)} = z^{(i)} - \eta \nabla h(z^{(i)})\]

Las mismas consideraciones acerca del tamaño de paso \(\eta\) aplican en el problema multivariado.

h <- function(z) {
  z[1]^2 + z[2]^2 - z[1] * z[2]
}
h_gr <- function(z_1,z_2) apply(cbind(z_1, z_2), 1, h)

grid_graf <- expand.grid(z_1 = seq(-3, 3, 0.1), z_2 = seq(-3, 3, 0.1))
grid_graf <- grid_graf %>%  mutate( val = h_gr(z_1, z_2) )
gr_contour <- ggplot(grid_graf, aes(x = z_1, y = z_2, z = val)) + 
  geom_contour(binwidth = 1.5, aes(colour = ..level..))
gr_contour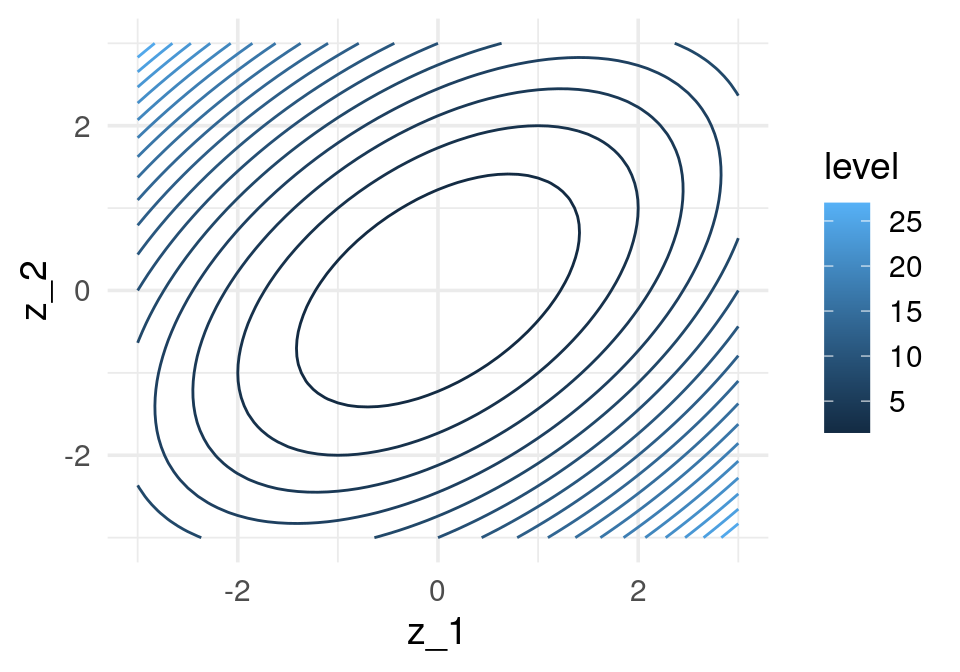

El gradiente está dado por (calculado a mano):

h_grad <- function(z){
  c(2*z[1] - z[2], 2*z[2] - z[1])
}

Podemos graficar la dirección de máximo descenso para diversos puntos. Estas direcciones son ortogonales a la curva de nivel que pasa por cada uno de los puntos:

grad_1 <- h_grad(c(0,-2))
grad_2 <- h_grad(c(1,1))
eta <- 0.2
gr_contour +
  geom_segment(aes(x = 0.0, xend = 0.0 - eta * grad_1[1], y = -2, yend = -2 - eta * grad_1[2]),
    arrow = arrow(length = unit(0.2, "cm"))) + 
  geom_segment(aes(x = 1, xend = 1 - eta * grad_2[1], y = 1, yend = 1 - eta*grad_2[2]),
    arrow = arrow(length = unit(0.2, "cm"))) + coord_fixed(ratio = 1)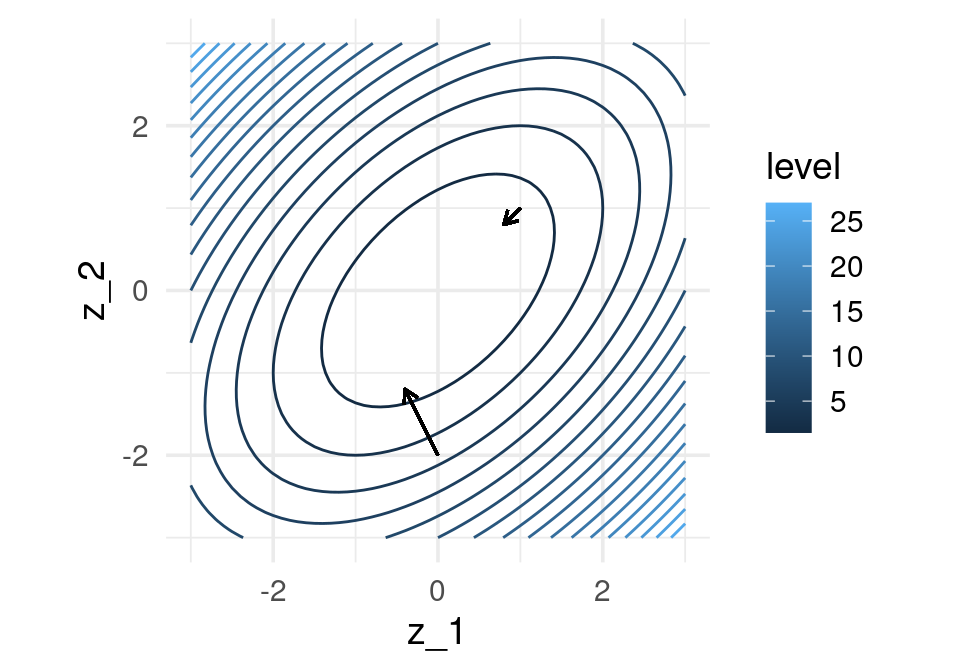

Y aplicamos descenso en gradiente:

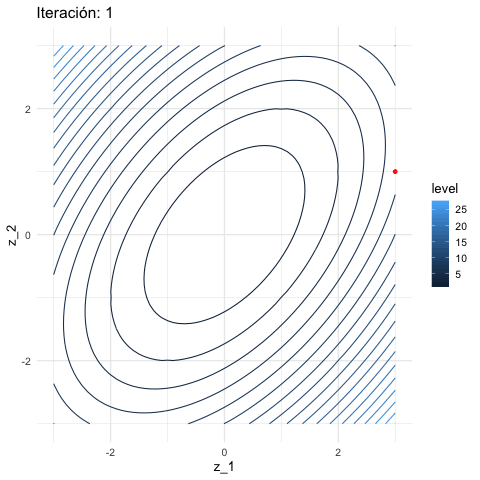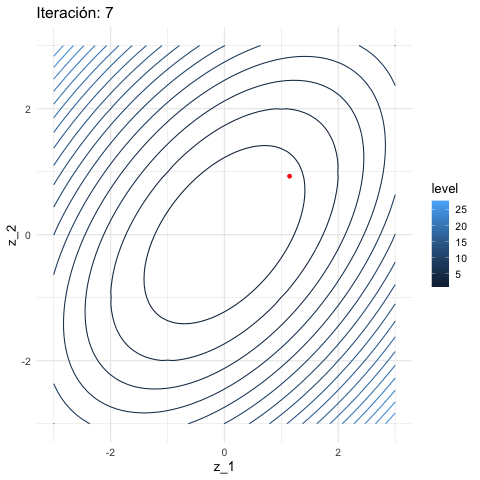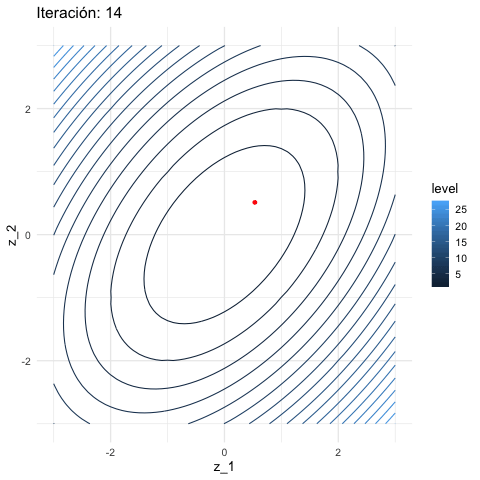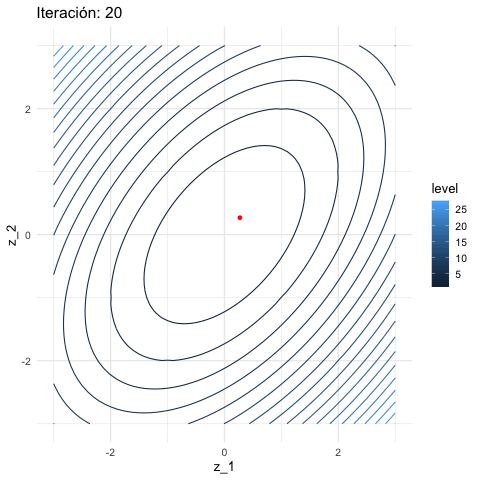
inicial <- c(3, 1)
iteraciones <- descenso(150, inicial , 0.1, h_grad)
df_iteraciones <- data.frame(iteraciones) %>%
    mutate(iteracion = 1:nrow(iteraciones))
graf_descenso_2 <- ggplot(data = df_iteraciones %>% filter(iteracion < 20)) + 
  geom_contour(data = grid_graf, 
               binwidth = 1.5, aes(x = z_1, y = z_2, z = val, colour = ..level..)) + 
  geom_point(aes(x=X1, y=X2), colour = 'red', size = 3)
if(FALSE){
    library(gganimate)
    graf_descenso_2 + 
        labs(title = 'Iteración: {frame_time}') +
        transition_time(iteracion)
    anim_save(filename = "figuras/descenso_2.gif")
}

En este caso, para checar convergencia podemos monitorear el valor de la función objetivo:

df_iteraciones <- df_iteraciones %>% 
    mutate(h_valor = map2_dbl(X1, X2, ~ h(z  = c(.x,.y)))) # h no está vectorizada
ggplot(df_iteraciones, aes(x = iteracion, y = h_valor)) + geom_point(size=1) +
    geom_line()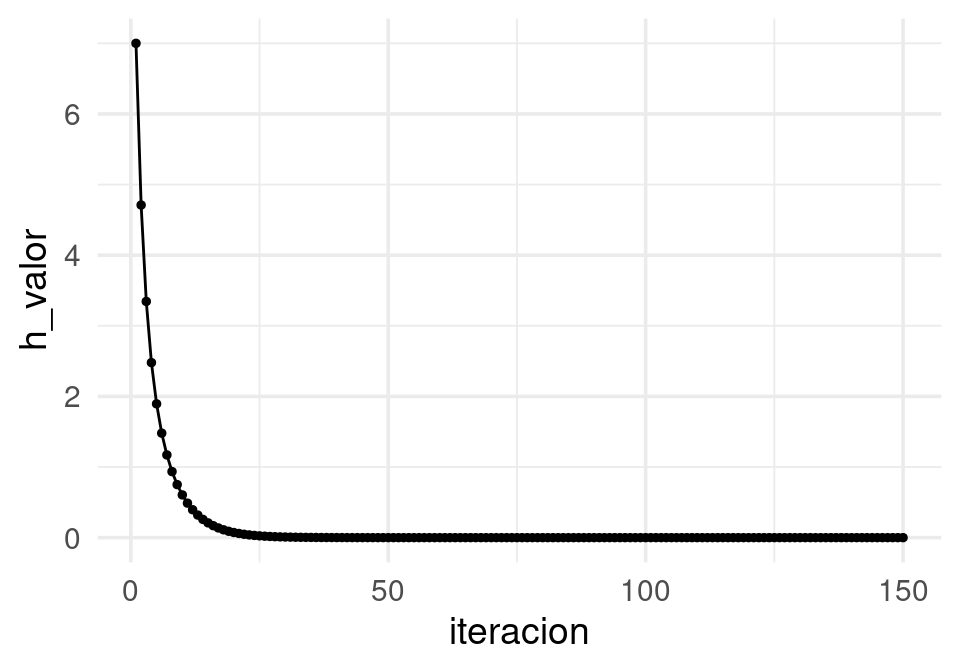

Y nuestra aproximación al mínimo es:

df_iteraciones %>% tail(1)

##               X1           X2 iteracion      h_valor
## 150 3.042033e-07 3.042033e-07       150 9.253964e-14

2.4.1 Cálculo del gradiente

Vamos a escribir ahora el algoritmo de descenso en gradiente para regresión lineal. Igual que en los ejemplos anteriores, tenemos que precalcular el gradiente. Una vez que esto esté terminado, escribir la iteración es fácil.

Recordamos que queremos minimizar (dividiendo entre dos para simplificar más adelante) \[L(\beta) = \frac{1}{2N}\sum_{i=1}^N (y^{(i)} - f_\beta(x^{(i)}))^2\]

La derivada de la suma es la suma de las derivadas, así nos concentramos en derivar uno de los términos

\[ u^{(i)}=\frac{1}{2}(y^{(i)} - f_\beta(x^{(i)}))^2 \] Usamos la regla de la cadena para obtener \[ \frac{1}{2}\frac{\partial}{\partial \beta_j} (y^{(i)} - f_\beta(x^{(i)}))^2 = -(y^{(i)} - f_\beta(x^{(i)})) \frac{\partial f_\beta(x^{(i)})}{\partial \beta_j}\]

Ahora recordamos que \[f_{\beta} (x) = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \cdots + \beta_p x_p\]

Y vemos que tenemos dos casos. Si \(j=0\),

\[\frac{\partial f_\beta(x^{(i)})}{\partial \beta_0} = 1\] y si \(j=1,2,\ldots, p\) entonces

\[\frac{\partial f_\beta(x^{(i)})}{\partial \beta_j} = x_j^{(i)}\]

Entonces, si ponemos \(u^{(i)}=\frac{1}{2}(y^{(i)} - f_\beta(x^{(i)}))^2\):

\[\frac{\partial u^{(i)}}{\partial \beta_0} = -(y^{(i)} - f_\beta(x^{(i)}))\] y

\[\frac{\partial u^{(i)}}{\partial \beta_j} = - x_j^{(i)}(y^{(i)} - f_\beta(x^{(i)}))\]

Y sumando todos los términos (uno para cada caso de entrenamiento):

Gradiente para regresión lineal Sea \(e^{(i)} = y_{(i)} - f_{\beta} (x^{(i)})\). Entonces \[\begin{equation} \frac{\partial L(\beta)}{\partial \beta_0} = - \frac{1}{N}\sum_{i=1}^N e^{(i)} \tag{2.1} \end{equation}\] \[\begin{equation} \frac{\partial L(\beta)}{\partial \beta_j} = - \frac{1}{N}\sum_{i=1}^N x_j^{(i)}e^{(i)} \tag{2.2} \end{equation}\] para \(j=1,2,\ldots, p\).

Nótese que cada punto de entrenamiento contribuye al cálculo del gradiente - la contribución es la dirección de descenso de error para ese punto particular de entrenamiento. Nos movemos entonces en una dirección promedio, para intentar hacer el error total lo más chico posible.

2.4.2 Implementación

En este punto, podemos intentar una implementación simple basada en el código anterior para hacer descenso en gradiente para nuestro problema de regresión (es un buen ejercicio). En lugar de eso, mostraremos cómo usar librerías ahora estándar para hacer esto. En particular usamos keras (con tensorflow), que tienen la ventaja:

En tensorflow y keras no es necesario calcular las derivadas a mano. Utiliza diferenciación automática, que no es diferenciación numérica ni simbólica: se basa en la regla de la cadena y la codificación explícita de las derivadas de funciones elementales.

library(keras)
# definición de estructura del modelo (regresión lineal)
x_ent <- casas_receta %>% prep %>% juice %>% select(tiene_piso_2, calidad) %>% as.matrix()
y_ent <- casas_receta %>% prep %>% juice %>% pull(precio_m2_miles)
n_entrena <- nrow(x_ent)
crear_modelo <- function(lr = 0.05){
    modelo_casas <- 
        keras_model_sequential() %>%
        layer_dense(units = 1,        #una sola respuesta,
            activation = "linear",    # combinar variables linealmente
            kernel_initializer = initializer_constant(0), #inicializamos coeficientes en 0
            bias_initializer = initializer_constant(0))   #inicializamos ordenada en 0
    # compilar seleccionando cantidad a minimizar, optimizador y métricas
    modelo_casas %>% compile(
        loss = "mean_squared_error",  # pérdida cuadrática
        optimizer = optimizer_sgd(lr = lr), # descenso en gradiente
        metrics = list("mean_squared_error"))
    modelo_casas
}
modelo_casas <- crear_modelo()
# Ahora iteramos
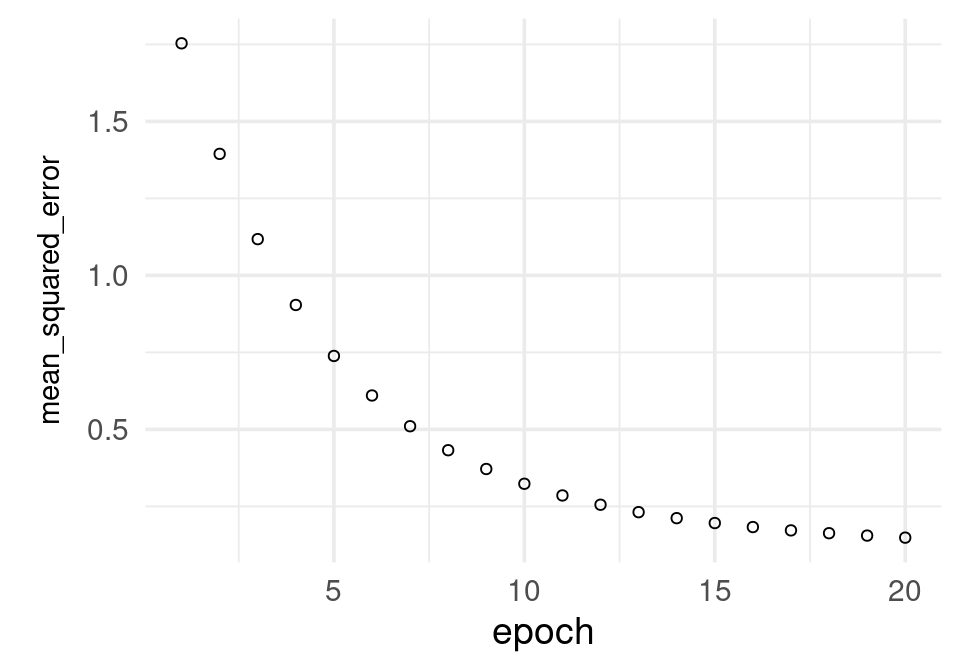
# Primero probamos con un número bajo de iteraciones
historia <- modelo_casas %>% fit(
  as.matrix(x_ent), # x entradas
  y_ent,            # y salida o target
  batch_size = nrow(x_ent), # para descenso en gradiente
  epochs = 20, # número de iteraciones
  verbose = 0
)

plot(historia, metrics = "mean_squared_error", smooth = FALSE)

# Agregamos iteraciones: esta historia comienza en los últimos valores de
# la corrida anterior
historia <- modelo_casas %>% fit(
  as.matrix(x_ent), # x entradas
  y_ent,            # y salida o target
  batch_size = nrow(x_ent), # para descenso en gradiente
  epochs = 1000, # número de iteraciones
  verbose = 0
)

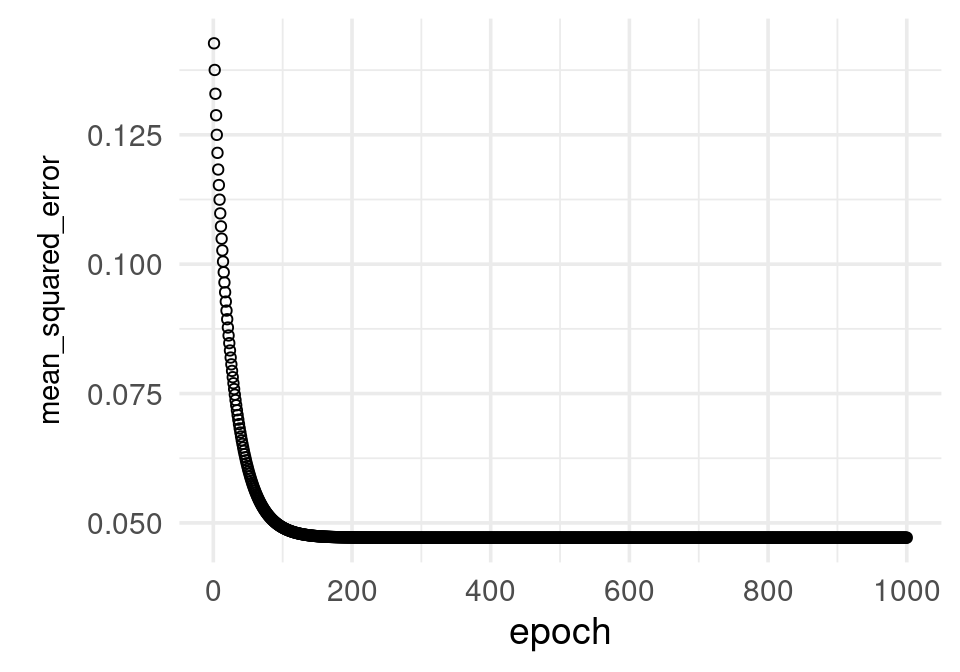
plot(historia, metrics = "mean_squared_error", smooth = FALSE)

El modelo parece todavía ir mejorando: puede dificil juzgar de esta gráfica. Veamos de todas formas los coeficientes estimados hasta ahora:

get_weights(modelo_casas)

## [[1]]
##            [,1]
## [1,] -0.3582432
## [2,]  0.1220758
## 
## [[2]]
## [1] 1.442377

La implementación oficial de R es lm, que en general tiene buen desempeño para datos que caben en memoria:

lm(precio_m2_miles ~ calidad + tiene_piso_2, data = train_tbl) %>% coef

##  (Intercept)      calidad tiene_piso_2 
##    1.4423781    0.1220760   -0.3582449

2.5 Normalización de entradas

La convergencia de descenso en gradiente (y también el desempeño numérico para otros algoritmos) puede dificultarse cuando las variables tienen escalas muy diferentes. Esto produce curvaturas altas en la función que queremos minimizar.

En este ejemplo simple, una variable tiene desviación estándar 10 y otra 1:

x1 <- rnorm(100, 0, 5) 
x2 <- rnorm(100, 0, 1) +  0.1*x1
y <- 0*x1 + 0*x2 + rnorm(100, 0, 0.1) 
dat <- tibble(x1, x2,  y)
rss <- function(beta)  mean((as.matrix(dat[, 1:2]) %*% beta - y)^2) 
grid_beta <- expand.grid(beta1 = seq(-1, 1, length.out = 50), 
                         beta2 = seq(-1, 1, length.out = 50))
rss_1 <- apply(grid_beta, 1, rss) 
dat_x <- data.frame(grid_beta, rss_1)
ggplot(dat_x, aes(x = beta1, y = beta2, z = rss_1)) + 
    geom_contour(binwidth = 0.5) +
    coord_equal()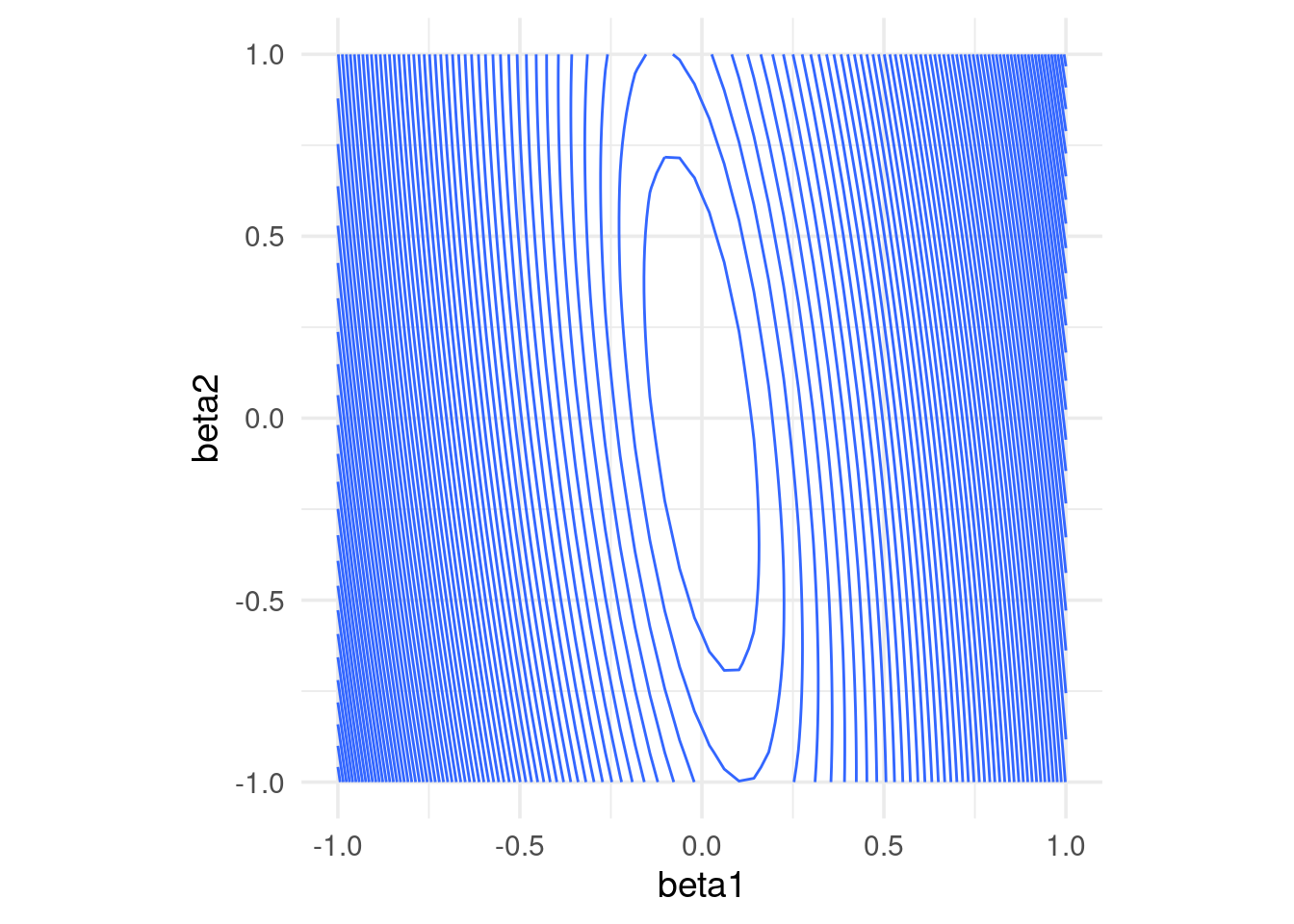

En algunas direcciones el gradiente es muy grande, y en otras chico. Esto implica que la convergencia puede ser muy lenta en algunas direcciones, puede diverger en otras, y que hay que ajustar el paso \(\eta > 0\) con cuidado, dependiendo de dónde comiencen las iteraciones.

Por ejemplo, con un tamaño de paso relativamente chico, damos unos saltos grandes al principio y luego avanzamos muy lentamente:

grad_calc <- function(x_ent, y_ent){
  # calculamos directamente el gradiente
  salida_grad <- function(beta){
    n <- length(y_ent)
    f_beta <- as.matrix(cbind(1, x_ent)) %*% beta
    e <- y_ent - f_beta
    grad_out <- - as.numeric(t(cbind(1, x_ent)) %*% e) / n
    names(grad_out) <- c('Intercept', colnames(x_ent))
    grad_out
  }
  salida_grad
}
grad_sin_norm <- grad_calc(dat[, 1:2, drop = FALSE], dat$y)
iteraciones <- descenso(10, c(0, -0.25, -0.75), 0.02, grad_sin_norm)
ggplot(dat_x) + 
    geom_contour(aes(x = beta1, y = beta2, z = rss_1), binwidth = 0.5) +
    coord_equal() +
  geom_path(data = data.frame(iteraciones[, 2:3]), aes(x=X1, y=X2), colour = 'red') +
  geom_point(data = data.frame(iteraciones[, 2:3]), aes(x=X1, y=X2), colour = 'red')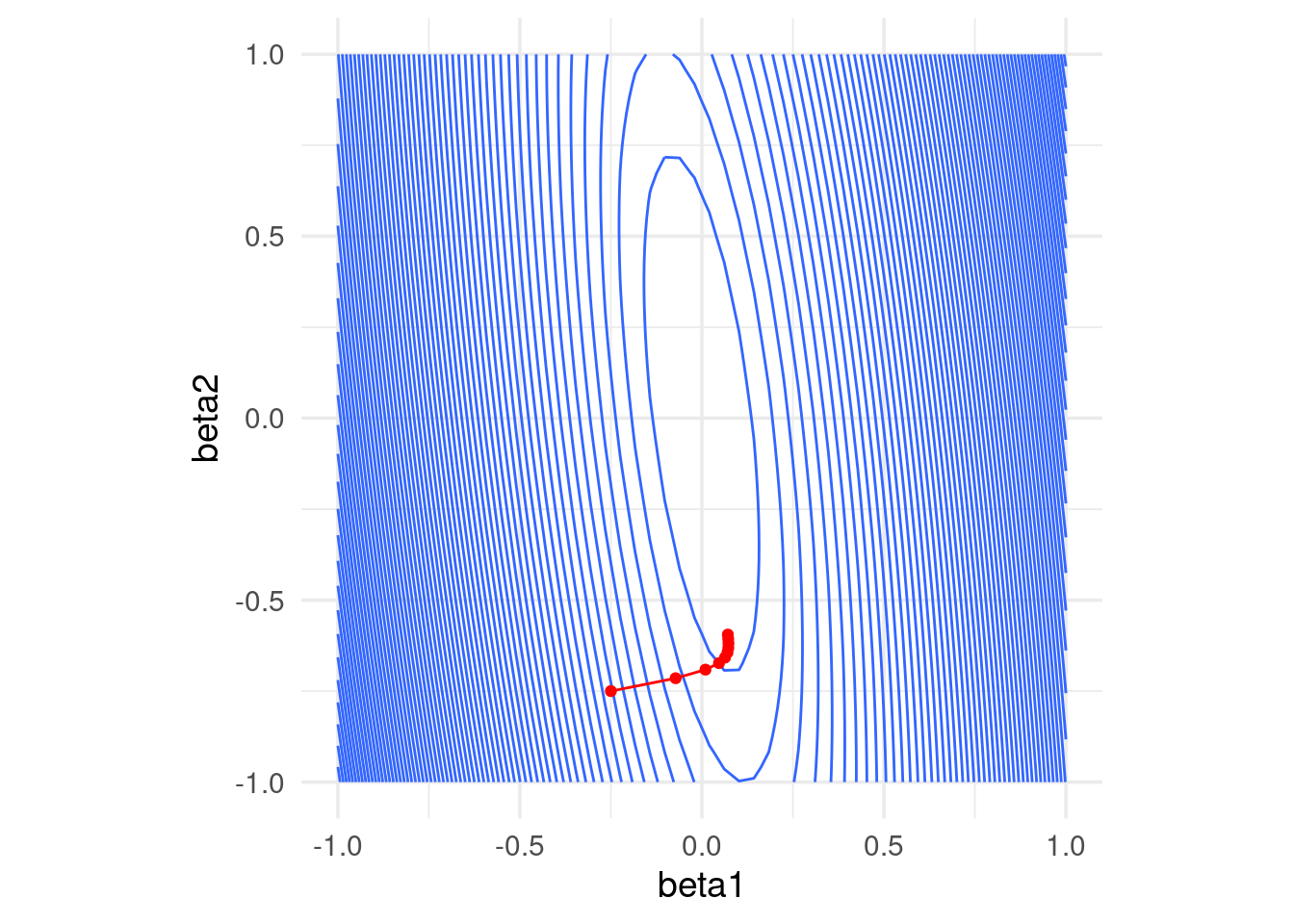

Si incrementamos el tamaño de paso observamos también convergencia lenta. En este caso particular, subir más el tamaño de paso puede producir divergencia:

iteraciones <- descenso(10, c(0, -0.25, -0.75), 0.07, grad_sin_norm)
ggplot(dat_x) + 
    geom_contour(aes(x = beta1, y = beta2, z = rss_1), binwidth = 0.5) +
    coord_equal() +
  geom_path(data = data.frame(iteraciones[, 2:3]), aes(x=X1, y=X2), colour = 'red') +
  geom_point(data = data.frame(iteraciones[, 2:3]), aes(x=X1, y=X2), colour = 'red')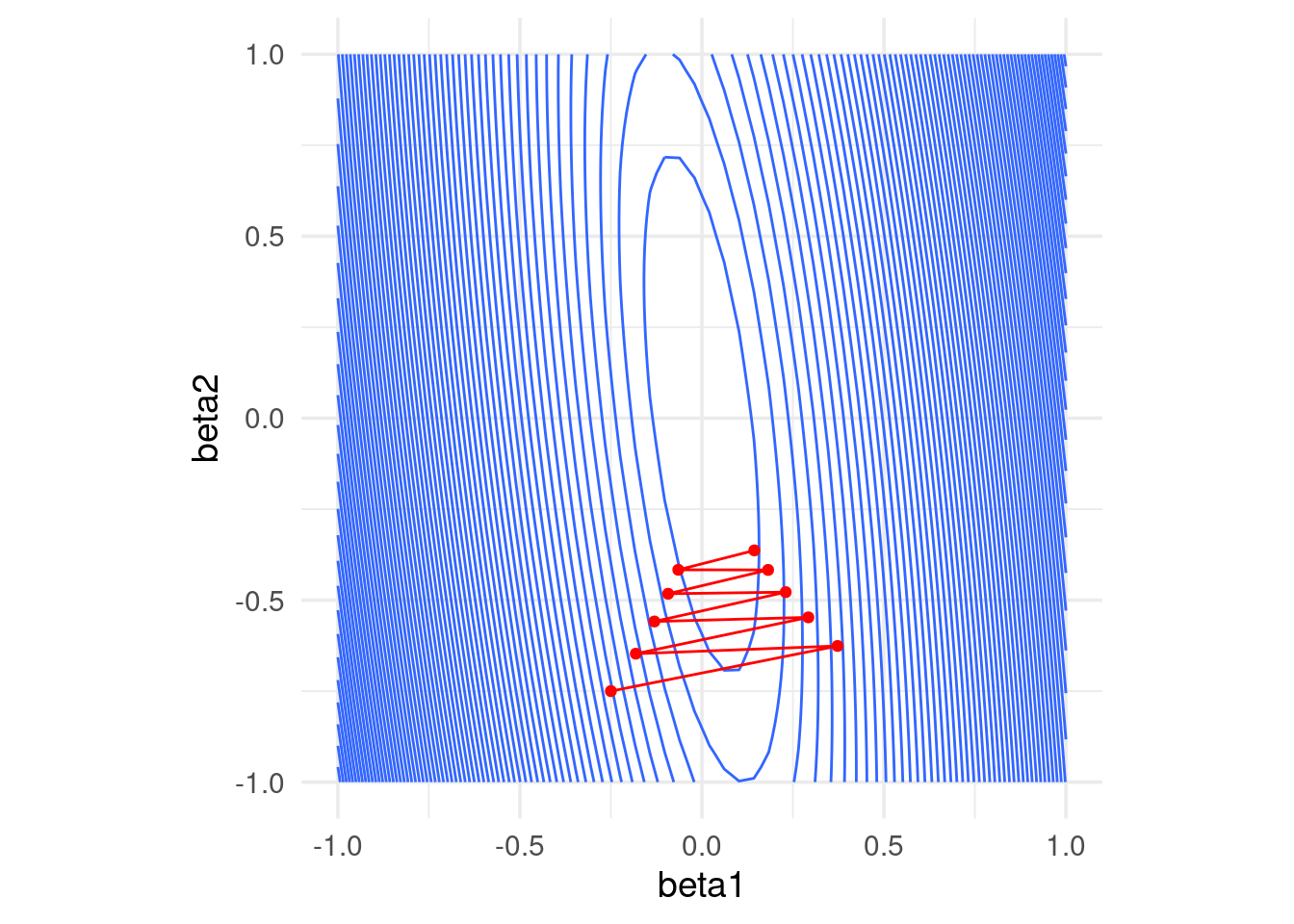

Una normalización usual es con la media y desviación estándar, donde hacemos, para cada variable de entrada \(j=1,2,\ldots, p\) \[ x_j^{(i)} = \frac{ x_j^{(i)} - \bar{x}_j}{s_j}\] donde \[\bar{x}_j = \frac{1}{N} \sum_{i=1}^N x_j^{(i)}\] \[s_j = \sqrt{\frac{1}{N-1}\sum_{i=1}^N (x_j^{(i)}- \bar{x}_j )^2}\] es decir, centramos y normalizamos por columna. Otra opción común es restar el mínimo y dividir entre la diferencia del máximo y el mínimo, de modo que las variables resultantes toman valores en \([0,1]\).

Entonces escalamos antes de ajustar:

x1_s = (x1 - mean(x1))/sd(x1)
x2_s = (x2 - mean(x2))/sd(x2)
dat <- data_frame(x1_s, x2_s,  y)

## Warning: `data_frame()` is deprecated as of tibble 1.1.0.
## Please use `tibble()` instead.
## This warning is displayed once every 8 hours.
## Call `lifecycle::last_warnings()` to see where this warning was generated.

rss <- function(beta)  mean((as.matrix(dat[, 1:2]) %*% beta - y)^2) 
grid_beta <- expand.grid(beta1 = seq(-1, 1, length.out = 50), 
                         beta2 = seq(-1, 1, length.out = 50))
rss_1 <- apply(grid_beta, 1, rss) 
dat_x <- data.frame(grid_beta, rss_1)
ggplot(dat_x, aes(x = beta1, y = beta2, z = rss_1)) + 
    geom_contour(binwidth = 0.5) +
    coord_equal()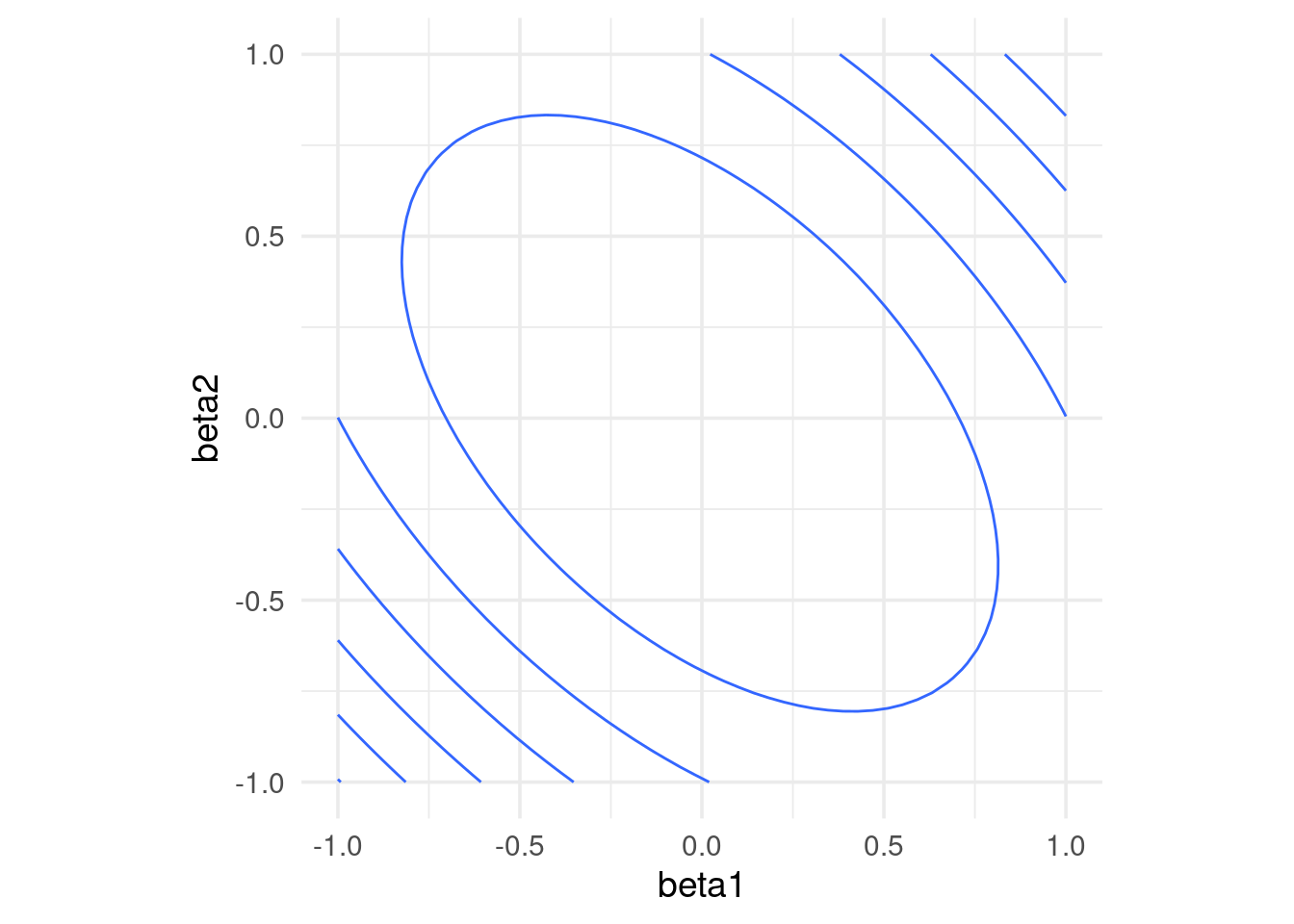

Nótese que los coeficientes ajustados serán diferentes a los del caso no normalizado.

Si normalizamos, obtenemos convergencia más rápida

grad_sin_norm <- grad_calc(dat[, 1:2, drop = FALSE], dat$y)
iteraciones <- descenso(10, c(0, -0.25, -0.75), 0.5, grad_sin_norm)
ggplot(dat_x) + 
    geom_contour(aes(x = beta1, y = beta2, z = rss_1), binwidth = 0.5) +
    coord_equal() +
  geom_path(data = data.frame(iteraciones[, 2:3]), aes(x=X1, y=X2), colour = 'red') +
  geom_point(data = data.frame(iteraciones[, 2:3]), aes(x=X1, y=X2), colour = 'red')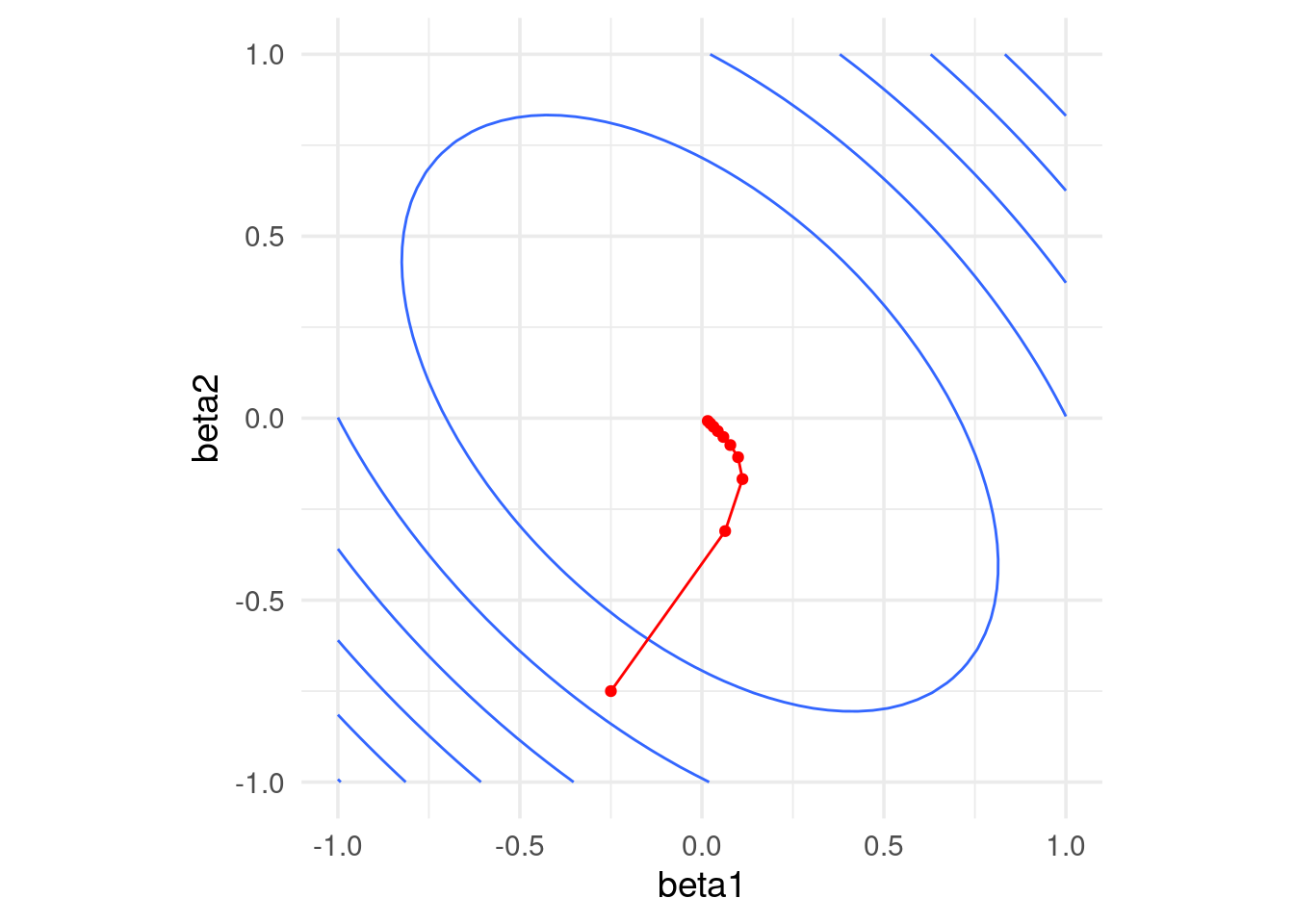

Cuando normalizamos antes de ajustar el modelo, las predicciones deben hacerse con entradas normalizadas. La normalización se hace con los mismos valores que se usaron en el entrenamiento (y no recalculando medias y desviaciones estándar con el conjunto de prueba). En cuanto a la forma funcional del predictor \(f\), el problema con entradas normalizadas es equivalente al de las entradas no normalizadas. Asegúrate de esto escribiendo cómo correponden los coeficientes de cada modelo normalizado con los coeficientes del modelo no normalizado.

Supongamos que el modelo en las variables originales es \[{f}_\beta (X) = \beta_0 + \beta_1 X_1 + \beta_2 X_2 + \cdots + \beta_p X_p,\] Consideramos el modelo con variables estandarizadas \[{g}_{\beta^s} (X) = \beta_0^s + \beta_1^s Z_1 + \beta_2^s Z_2 + \cdots + \beta_p^s Z_p,\]

Sustituyendo \(Z_j = (X_j - \mu_j)/s_j,\)

\[{g}_{\beta^s} (X) = (\beta_0^s - \sum_{j=1}^p \beta_j^s \mu_j/s_j) + \frac{\beta_1^s}{s_j} X_1 + \frac{\beta_2^s}{s_2} X_2 + \cdots + \frac{\beta_p^s}{s_p} X_p,\] Y vemos que tiene la misma forma funcional de \(f_\beta(X)\). Si la solución de mínimos cuadrados es única, entonces una vez que ajustemos tenemos que tener \(\hat{f}_\beta(X) = \hat{g}_{\beta^s} (X)\), lo que implica que \[\hat{\beta}_0 = \hat{\beta}_0^s - \sum_{j=1}^p \hat{\beta}_j^s\mu_j/s_j\] y \[\hat{\beta}_j = \hat{\beta}_j^s/s_j.\]

Nótese que para pasar del problema estandarizado al no estandarizado simplemente se requiere escalar los coeficientes por la \(s_j\) correspondiente.

Ejemplo

Repetimos nuestro modelo

library(keras)
# definición de estructura del modelo (regresión lineal)
n_entrena <- nrow(x_ent)
x_ent_s <- scale(x_ent)
ajustar_casas <- function(modelo, x, y, n_epochs = 100){
  ajuste <- modelo %>% fit(
    as.matrix(x), y,
    batch_size = nrow(x_ent), # para descenso en gradiente
    epochs = n_epochs, # número de iteraciones
    verbose = 0) %>% as_tibble()
  ajuste
}
modelo_casas_ns <- crear_modelo(0.07)
modelo_casas_s <- crear_modelo(0.2)
historia_s <- ajustar_casas(modelo_casas_s, x_ent_s, y_ent) %>% 
  mutate(tipo = "Estandarizar")
historia_ns <- ajustar_casas(modelo_casas_ns, x_ent, y_ent) %>% 
  mutate(tipo = "Sin estandarizar")
historia <- bind_rows(historia_ns, historia_s) %>%  filter(metric == "mean_squared_error")
ggplot(historia, aes(x = epoch, y = value, colour = tipo)) +
     geom_line() + geom_point() +scale_x_log10() + scale_y_log10()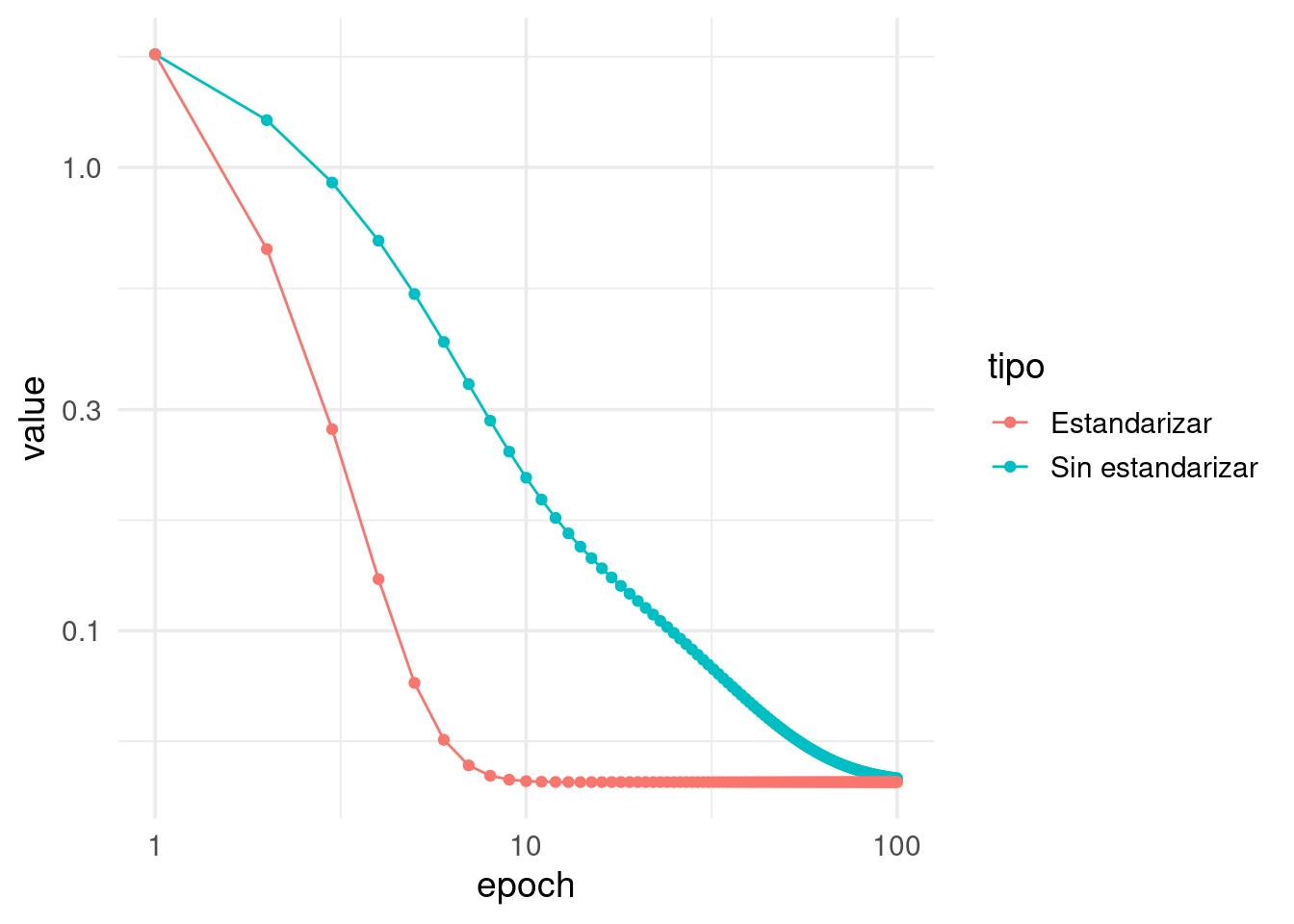

Observamos que el modelo con datos estandarizados convergió:

get_weights(modelo_casas_s)

## [[1]]
##            [,1]
## [1,] -0.1772382
## [2,]  0.1610471
## 
## [[2]]
## [1] 1.288718

coef(lm.fit(cbind(1,x_ent_s), y_ent))

##              tiene_piso_2      calidad 
##    1.2887179   -0.1772382    0.1610471

Mientras que el modelo no estandarizado todavía requiere iteraciones:

get_weights(modelo_casas_ns)

## [[1]]
##            [,1]
## [1,] -0.2991632
## [2,]  0.1169387
## 
## [[2]]
## [1] 1.41126

coef(lm.fit(cbind(1, x_ent), y_ent))

##              tiene_piso_2      calidad 
##    1.4423781   -0.3582449    0.1220760

2.6 Interpretación de modelos lineales

Muchas veces se considera que la facilidad de interpretación es una fortaleza del modelo lineal. Esto es en parte cierto, pero hay algunas consideraciones importantes que debemos tomar en cuenta.

En primer lugar, podemos separar la interpretación en dos modalidades:

Entender cómo calcula nuestro modelo las predicciones.
Entender aspectos del fenómeno de interés a través de nuestro modelo. Por ejemplo, interpretar un coeficiente positivo como el efecto en nuevos datos de cambiar una variable que podemos manipular.

Las interpretaciones del tipo 1 son en general simples para modelos lineales, y sirven para explicar la estructura del modelo. Para modelos más complicados es necesario usar herramientas más complejas (que veremos más adelante).

Sin embargo, las interpretaciones de tipo 2 están llenas de dificultades, incluso si utilizamos modelos lineales. Tenemos que recordar que el modelo, aunque tiene una forma simple, generamente está construido con datos que distan mucho de ser simples, y que patrones inesperados en esos datos que tienen que ver con el proceso generador de datos convierte la tarea de predicción en este segundo sentido en una tarea muy difícil.

Con datos observaciones (no experimentales), los modelos lineales también son cajas negras, pues es necesario entender la complejidad de los datos (generalmente alta complejidad) para interpretar correctamente los coeficientes.

Ejemplo

Consideramos otro modelo para estudiar su estructura:

train_tbl <- train_tbl %>% mutate(habitable_100_m2_c = (habitable_m2 - mean(habitable_m2))/100)
modelo_casas <- lm( precio_m2_miles ~ 1 + calidad + tiene_piso_2 + habitable_100_m2_c, data = train_tbl)
# interpretar en miles de dólares
cat("Coeficientes para precio por metro cuadrado \n")
## Coeficientes para precio por metro cuadrado
1000*(coef(modelo_casas) %>% round(2))
##        (Intercept)            calidad       tiene_piso_2 habitable_100_m2_c 
##               1400                160               -250               -240

La ordenada al origen se interpreta como sigue: para calidad media (calidad = 6), y tamaño promedio (habitable_100_m2_c = 0), en un una casa que no tiene 2 pisos, la predicción es de 1400 dólares por m2.
El coeficiente de calidad: dejando fijo tiene_piso_2 y tamaño, la predicción de precio por m2 aumenta en 170 dólares adicionales por cada punto que sube la calidad.
El coeficiente de tiene_piso_2: dejando constante la calidad y el tamaño, la predicción de precio por m2 baja en 260 dólares si la casa tiene 2 pisos en lugar de 1.
El coeficiente de habitable_100_m2_c: dejando constante la calidad y el número de pisos, la predicción de precio por m2 baja en 270 dólares por cada 100 m2 adicionales de tamaño de la casa.

Así podemos explicar cada predicción - considerando qué variables aportan positiva y cuáles negativamente a la predicción, cuando mantenemos el resto constante. El camino más seguro es limitarse a hacer este tipo de análisis de las predicciones. Hablamos de entender la estructura predictiva del problema con los datos que tenemos - y no intentamos ir hacia la explicación del fenómeno.

Cualquier otra interpretación requiere mucho más cuidados, y requiere una revisión de la especificación correcta del modelo. Parte de estos cuidados se estudian en un curso de regresión desde el punto de vista estadístico, por ejemplo:

Efectos no lineales (especificación incorrecta del modelo): si la estructura del problema es altamente no lineal, los coeficientes de un modelo lineal no tienen una interpretación clara en relación al fenómeno.
La interpretación coeficiente a coeficiente no toma en cuenta la estructura de asociación de las \(x's\). Rara vez cambios marginales en una variable de entrada ocurren de manera independiente de las otras variables de entrada. Eso hace difícil de interpretar los coeficientes.
Variación muestral. Es necesario en primer lugar considerar la variación en nuestras estimaciones de los coeficientes para poder concluir acerca de su relación con el fenómeno (tratable desde punto de vista estadístico, pero hay que checar supuestos).

Otros cuidados adicionales, aún más sutiles e importantes, se requieren si queremos hacer afirmaciones causales: ¿qué pasaría si diseñáramos una intervención para cambiar una característica de las unidades? ¿qué nos dice modelos acerca del cambio en la variable respuesta?

Variables omitidas: si nos faltan algunas variables cruciales en el fenómeno que nos interesa, o el modelo sufre de otro tipo de especificación incorrecta , puede ser muy difícil interpretar los coeficientes en términos del fenómeno. Por ejemplo:

Ejemplo: ¿interpretación causal?

Supongamos que queremos predecir cuánto van a gastar en televisiones samsung ciertas personas que llegan a Amazon. Una variable de entrada es el número de anuncios de televisiones Samsung que recibieron antes de llegar a Amazon. El coeficiente de esta variable es alto (significativo, etc.), así que concluimos que el anuncio causa compras de televisiones Samsung.

¿Qué está mal aquí? Cuando las personas están investigando acerca de televisiones, reciben anuncios. La razón es que esta variable nos puede indicar más bien quién está en proceso de compra de una televisión samsung (reciben anuncios) y quién no (no hacen búsquedas relevantes, así que no reciben anuncios). El modelo está mal especificado porque no consideramos que hay otra variable importante, que es el interés de la persona en compra de TVs Samsung. Sin embargo, ningún diagnóstico del modelo nos puede decir de esta especificación incorrecta.

Notamos otro ejemplo en nuestro análisis anterior. Si consideramos el modelo simple para precio en miles de dólares:

modelo_casas_1 <- lm( precio_miles ~ 1 + habitaciones, data = train_tbl)
(coef(modelo_casas_1) %>% round(2))

##  (Intercept) habitaciones 
##       121.04        19.07

¿Esto implica entonces que mejorar el valor de una casa conviene dividir habitaciones? Probablemente no. Por ejemplo, para un tamaño de casa fijo, el coeficiente de número de habitaciones es negativo.

modelo_casas_2 <- lm( precio_miles ~ 1 + calidad + habitaciones + habitable_100_m2_c , data = train_tbl)
(coef(modelo_casas_2) %>% round(2))

##        (Intercept)            calidad       habitaciones habitable_100_m2_c 
##             217.59              25.31             -14.56              87.60

Para construir modelos apropiados e interpretaciones adecuadas se requiere tener las variables y datos importantes, los modelos correctos tanto en términos estadísticos como en términos de conocimiento de dominio, y entender cómo es el proceso generador de los datos que estamos utilizando. En general, la recomendación es que las interpretaciones causales deben considerarse como preliminares bajo ciertos supuestos, y se requiere más análisis y consideraciones antes de poder tener interpretaciones causales sólidas (ver Imai, King, and Stuart (2008) y Gelman and Hill (2007), por ejemplo).

2.7 Predicción e incertidumbre

En todos los casos de arriba, vimos cómo hacer predicciones puntuales para minimizar el error de predicción. Como función de pérdida utilizamos el error cuadrático. Esto resulta en un problema tratable que se puede optimizar de manera escalable.

En problemas reales, sin embargo, rara vez estamos interesado en minimizar la pérdida cuadrática. Más bien queremos tomar una decisión más compleja en función de los datos. En esta situación, típicamente no es tan útil una predicción puntual, y quisiéramos saber qué tanta incertidumbre tenemos acerca de los posibles valores de \(y\), para cada predicción individual. Esto es especialmente cierto cuando observamos que el error cuadrático tiene tamaño considerable.

Por ejemplo: supongamos que estamos identificando clientes con valor alto (aquellos que predecimos que van a hacer compras grandes futuras) pues queremos diseñar una intervención para mejorar su satisfacción, mejorar su retención, o aumentar su valor de algún modo. Ahora imaginemos que tenemos dos clientes, cuya predicción es igual a 10,000. Sin embargo, tenemos incertidumbre alta acerca del cliente A (podría ir de 2 a 20 mil), mientras que para cliente B tenemos incertidumbre relativamente baja (por ejemplo, de 8 mil a 12 mil pesos). Si el tratamiento es costoso, puedes ser que preferamos tratar a B en lugar de A.

Otro ejemplo es si queremos hacer pronósticos de ventas o inventarios para tiendas individuales de una cadena de supermercados. En este caso, es difícil hacer planeación y evaluar el riesgo si solo tenemos predictores puntuales, y quisiéramos saber qué otros escenarios son consistentes con los datos, y cuánta incertidumbre tenemos en cada tienda individual. Aquí el error cuadrático es claramente insuficiente, pues el concepto de pérdidas y riesgos es mucho más complicado.

En estos casos, es importante construir, en lugar de predicciones puntuales, intervalos de predicción. Hay muchos enfoques para construir estos intervalos: puedes estudiarlo en un curso estándar de regresión, regresión bayesiana (ve por ejemplo Gelman and Hill (2007)), y también existen métodos computacionales basados en simulación de aplicación más general. Siempre es mejor tener intervalos construidos apropiadamente que no tenerlos, pero tenemos que considerar que esto requiere más esfuerzo y recursos, en particular:

Costo computacional adicional considerable y/o
Recaer en supuestos teóricos (muchas veces asintóticos) y diagnósticos de modelos, y
Validación adicional de modelos

En caso de producir intervalos, es importante de cualquier forma checar directamente que nuestros rangos de incertidumbre son apropiados (para lo cual también es útil muestras de prueba independientes del entrenamiento). Sin muestras de prueba, puede ser muy difícil evaluar qué tan buenas son nuestras estimaciones de la incertidumbre. Casi todos los modelos tienen fallas en este sentido.

Por otro lado, en algunas aplicaciones tener un error promedio razonable es suficiente, necesitamos tomar un número relativamente grande de decisiones, con costos relativamente uniformes (desde el punto de vista del negocio o de daños posibles) los estimadores puntuales pueden ser suficientes cuando el error de predicción es suficientemente bajo. Siempre revisa los errores individuales con la muestra prueba, y considera si es necesario calcular y checar intervalos predictivos.

Ejemplo

Para nuestro ejemplo de precios de casas, si queremos obtener intervalos de predicción razonables es necesario hacer ejercicios de modelación más delicados. En el siguiente ejemplo producimos intervalos de cobertura nominal del 95%. Con la muestra de prueba checamos que estos intervalos estén bien calibrados:

casas_int <- predict(ajuste, test_tbl, type = "pred_int", level = 0.95) %>% 
  bind_cols(predict(ajuste, test_tbl)) %>% 
  bind_cols(test_tbl) %>% 
  mutate(.pred_lower = .pred_lower * habitable_m2, 
         .pred = .pred * habitable_m2,
         .pred_upper = .pred_upper * habitable_m2,)
head(casas_int)

## # A tibble: 6 x 10
##   .pred_lower .pred_upper .pred    Id tiene_piso_2 precio_miles habitable_m2
##         <dbl>       <dbl> <dbl> <dbl>        <dbl>        <dbl>        <dbl>
## 1       129.         271.  200.     3            1         224.        166. 
## 2       184.         359.  271.     5            1         250         204. 
## 3        86.3        169.  128.    11            0         130.         96.6
## 4        94.7        174.  135.    17            0         149          93.3
## 5        92.8        196.  144.    18            0          90         120. 
## 6       117.         205.  161.    22            0         139.        103. 
## # … with 3 more variables: precio_m2_miles <dbl>, calidad <dbl>,
## #   habitaciones <dbl>

ggplot(casas_int, aes(x = .pred, ymin = .pred_lower, ymax = .pred_upper)) +
    geom_linerange(colour = "gray") +
    geom_point(aes(y = precio_miles), colour = "red")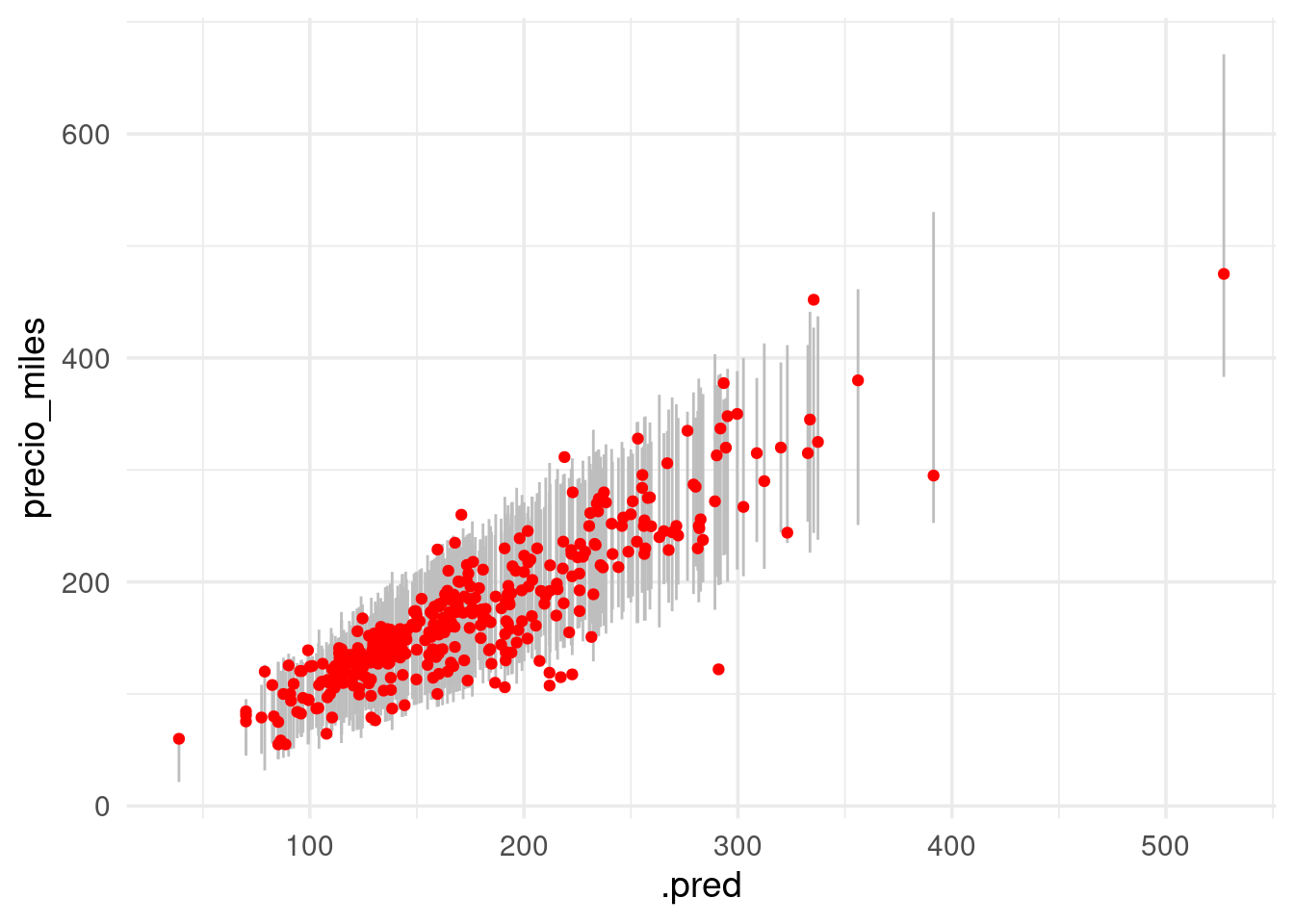

La cubertura se ve apropiada. Resumimos con:

casas_int %>% 
    mutate(cubre = precio_miles > .pred_lower & precio_miles < .pred_upper) %>% 
    summarise(cobertura = mean(cubre), 
              ee = sqrt(mean(cubre) * mean(1 - cubre) / n())) %>% 
    mutate(across(where(is.numeric), ~ round(.x, 3)))

## # A tibble: 1 x 2
##   cobertura    ee
##       <dbl> <dbl>
## 1     0.945 0.012