Clase 3 Métodos locales y regresión lineal

Regresión lineal es un método muy simple, y parecería que debería haber métodos más avanzados que lo superen fácilmente en la predicción.

Para empezar, es poco creíble que el modelo \[f(x) = b_0 + b_1x_1 + \cdots b_p x_p\] se cumple exactamente para el fenómeno que estamos tratando. Pero regresión lineal muchas veces supera a métodos que intentan construir predictores más complejos. Una de las primeras razones es que podemos ver la aproximación lineal como una aproximación de primer orden a la verdadera $f(x)$, y muchas veces eso es suficiente para producir predicciones razonables.

Adicionalmente, otras veces sólo tenemos suficientes datos para hacer una aproximación de primer orden, aún cuando la verdadera $f(x)$ no sea lineal, y resulta que esta aproximación da buenos resultados. Esto es particularmente cierto en problemas de dimensión alta, como veremos a continuación.

3.1 k vecinos más cercanos

Un método popular, con buen desempeño en varios ejemplos, es el de k-vecinos más cercanos, que consiste en hacer aproximaciones locales directas de $f(x)$. Sea ${\mathcal L}$ un conjunto de entrenamiento. Para $k$ entera fija, y $x_0$ una entrada donde queremos predecir, definimos a $N_k(x_0)$ como el conjunto de los $k$ elementos de ${\mathcal L}$ que tienen $x^{(i)}$ más cercana a $x_0$. Hacemos la predicción \[\hat{f}(x_0) = \frac{1}{k}\sum_{x^{(i)} \in N_k(x_0)} y^{(i)}\]

Es decir, promediamos las $k$ $y$’s con $x$’s más cercanas a donde queremos predecir.

Ejemplo

library(tidyverse)

## Warning: replacing previous import 'vctrs::data_frame' by 'tibble::data_frame'
## when loading 'dplyr'

auto <- read_csv("../datos/auto.csv")
datos <- auto[, c('name', 'weight','year', 'mpg', 'displacement')]
datos <- datos %>% mutate(
  peso_kg = weight * 0.45359237,
  rendimiento_kpl = mpg * (1.609344 / 3.78541178))
nrow(datos)

## [1] 392

Vamos a separa en muestra de entrenamiento y de prueba estos datos. Podemos hacerlo como sigue (2/3 para entrenamiento aproximadamente en este caso, así obtenemos alrededor de 100 casos para prueba):

library(tidymodels)

## Warning: package 'parsnip' was built under R version 4.0.3

set.seed(123)
datos_split <- initial_split(datos, prop = 0.7)
datos_entrena <- training(datos_split)
datos_prueba <- testing(datos_split)
nrow(datos_entrena)

## [1] 275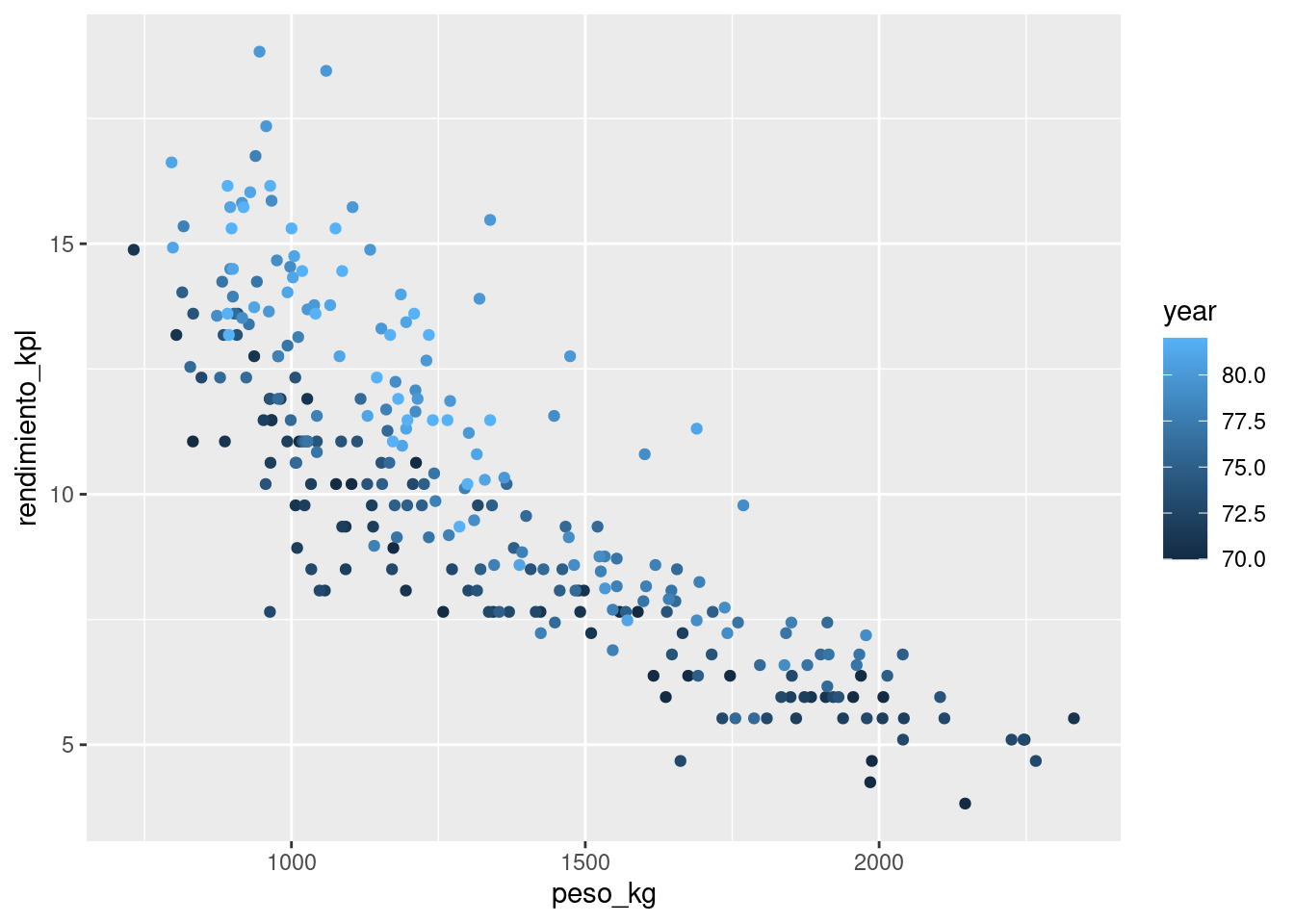

nrow(datos_prueba)

## [1] 117

ggplot(datos_entrena, aes(x = peso_kg, y = rendimiento_kpl, colour=year)) +
  geom_point()

Consideremos un modelo de $k=15$ vecinos más cercanos. La función de predicción ajustada es entonces:

# nótese que no normalizamos entradas - esto también es importante
# hacer cuando hacemos vecinos más cercanos, pues en otro caso
# las variables con escalas más grandes dominan el cálculo
vmc_1 <- nearest_neighbor(neighbors = 15, weight_func = "rectangular") %>% 
  set_engine("kknn") %>% 
  set_mode("regression")
receta_vmc <- recipe(rendimiento_kpl ~ peso_kg + year, datos_entrena) %>% 
  step_normalize(all_predictors()) %>% 
  prep()
flujo <- workflow() %>% 
  add_recipe(receta_vmc) 
ajuste_1 <- flujo %>% add_model(vmc_1) %>% fit(datos_entrena)

dat_graf <- tibble(peso_kg = seq(700, 2200, by = 10)) %>% 
  crossing(tibble(year= c(70, 75, 80)))
dat_graf <- dat_graf %>% 
  mutate(pred_1 = predict(ajuste_1, dat_graf) %>% pull(.pred))
ggplot(datos_entrena, aes(x = peso_kg, group = year, colour = year)) +
  geom_point(aes(y = rendimiento_kpl), alpha = 0.6) + 
  geom_line(data = dat_graf, aes(y = pred_1),  size = 1.2)

Y para $k=1$ vecinos más cercanos:

vmc_2 <- nearest_neighbor(neighbors = 1, weight_func = "rectangular") %>% 
  set_engine("kknn") %>% 
  set_mode("regression")
ajuste_2 <- flujo %>% add_model(vmc_2) %>% fit(datos_entrena)
dat_graf <- dat_graf %>% 
  mutate(pred_2 = predict(ajuste_2, dat_graf) %>% pull(.pred))
ggplot(datos_entrena, aes(x = peso_kg, group = year, colour = year)) +
  geom_point(aes(y = rendimiento_kpl), alpha = 0.6) + 
  geom_line(data = dat_graf, aes(y = pred_2),  size = 1.2)

En nuestro caso, los errores de prueba son

eval_1 <- predict(ajuste_1, datos_prueba) %>% 
  bind_cols(datos_prueba) %>% 
  rmse(rendimiento_kpl, .pred) %>% 
    mutate(n_vecinos = 15) 
eval_2 <- predict(ajuste_2, datos_prueba) %>% 
  bind_cols(datos_prueba) %>% 
  rmse(rendimiento_kpl, .pred) %>% 
    mutate(n_vecinos = 1) 
bind_rows(eval_1, eval_2)

## # A tibble: 2 x 4
##   .metric .estimator .estimate n_vecinos
##   <chr>   <chr>          <dbl>     <dbl>
## 1 rmse    standard        1.38        15
## 2 rmse    standard        1.61         1

Observaciones: - En ambos casos tenemos error de estimación del error de predicción. Cuando la muestra de prueba es relativamente chica, es importante estimar esta cantidad. - ¿Cómo escogerías una $k$ adecuada para este problema? Recuerda que adecuada significa que se reduzca a mínimo posible el error de predicción. Como ejercicio, compara los modelos con $k = 2, 25, 100$ utilizando una muestra de prueba. ¿Cuál se desempeña mejor? Da las razones de el mejor o peor desempeño: recuerda que el desempeño en predicción puede sufrir porque la función estimada no es suficiente flexible para capturar patrones importantes, pero también porque parte del ruido se incorpora en la predicción. Nota: no es muy conveniente utilizar el conjunto de prueba para seleccionar parámetros de nuestros métodos. Veremos más adelantes cómo hacer este paso usando una muestra o método de validación adicionales.

Por los ejemplos anteriores, vemos que k-vecinos más cercanos puede considerarse como un aproximador universal, que puede adaptarse a cualquier patrón importante que haya en los datos. Entonces, ¿cuál es la razón de utilizar otros métodos como regresión? ¿Por qué el desempeño de regresión sería superior?

3.2 La maldición de la dimensionalidad

El método de k-vecinos más cercanos funciona mejor cuando hay muchas $x$ cercanas a $x0$, de forma que el promedio sea estable (muchas $x$), y extrapolemos poco ($x$ cercanas). Cuando $k$ es muy chica, nuestras estimaciones son ruidosas, y cuando $k$ es grande y los vecinos están lejos, entonces estamos sesgando la estimación local con datos lejanos a nuestra región de interés.

El problema es que en dimensión alta, casi cualquier conjunto de entrenamiento (independientemente del tamaño) sufre fuertemente por uno o ambas dificultades del problema.

Ejemplo

Consideremos que la salida Y es determinística $Y = e^{-8\sum_{j=1}^p x_j^2}$. Vamos a usar 1-vecino más cercano para hacer predicciones, con una muestra de entrenamiento de 1000 casos. Generamos $x^{i}‘s uniformes en $[ 1,1]$, para $p = 2$, y calculamos la respuesta $Y$ para cada caso:

fun_exp <- function(x) exp(-8 * sum(x ^ 2))
x <- map(1:1000, ~ runif(2, -1, 1))
dat <- tibble(x = x) %>% 
        mutate(y = map_dbl(x, fun_exp))
ggplot(dat %>% mutate(x_1 = map_dbl(x, 1), x_2 = map_dbl(x, 2)), 
       aes(x = x_1, y = x_2, colour = y)) + geom_point()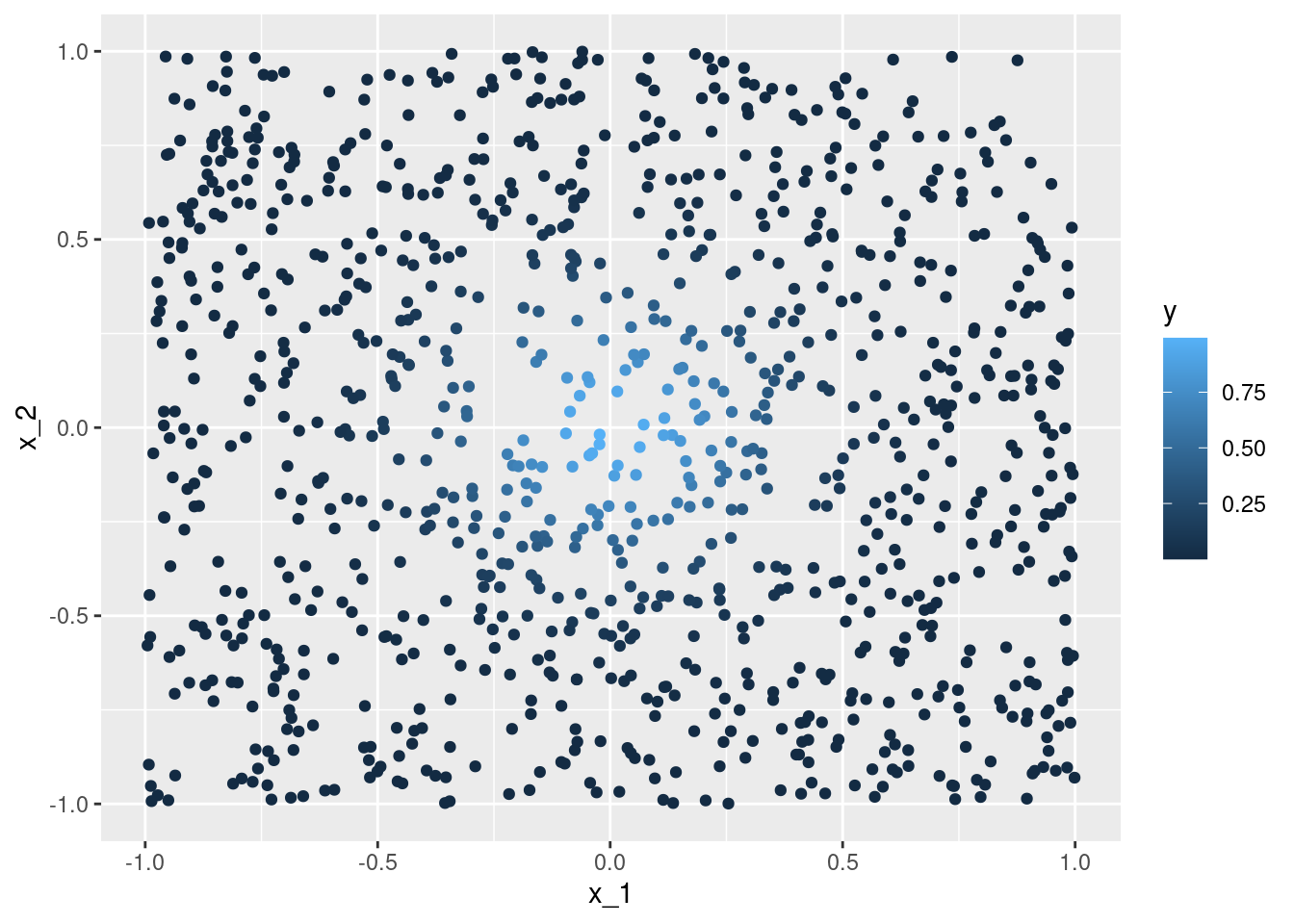

La mejor predicción en $x_0 = (0,0)$ es $f((0,0)) = 1$. El vecino más cercano al origen es

dat <- dat %>% mutate(dist_origen = map_dbl(x, ~ sqrt(sum(.x^2)))) %>% 
  arrange(dist_origen)
mas_cercano <- dat[1, ]
mas_cercano

## # A tibble: 1 x 3
##   x             y dist_origen
##   <list>    <dbl>       <dbl>
## 1 <dbl [2]> 0.993      0.0292

mas_cercano$x[[1]]

## [1] -0.02265293 -0.01844754

Nuestra predicción es entonces $\hat{f}(0)=$ 0.9931955, que es bastante cercano al valor verdadero (1).

Ahora intentamos hacer lo mismo para dimensión $p=8$.

x <- map(1:1000, ~ runif(8, -1, 1))
dat <- tibble(x = x) %>% 
       mutate(y = map_dbl(x, fun_exp))
dat <- dat %>% mutate(dist_origen = map_dbl(x, ~ sqrt(sum(.x^2)))) %>% 
  arrange(dist_origen)
mas_cercano <- dat[1, ]
mas_cercano

## # A tibble: 1 x 3
##   x              y dist_origen
##   <list>     <dbl>       <dbl>
## 1 <dbl [8]> 0.0278       0.669

mas_cercano$x[[1]]

## [1] -0.1344404151  0.0008044406 -0.0555683421  0.0352307903  0.5285954541
## [6]  0.3168313340 -0.1332451142 -0.1664795051

Y el resultado es un desastre. Nuestra predicción es

mas_cercano$y

## [1] 0.02783807

Necesitariamos una muestra de alrededor de un millón de casos para obtener resultados no tan malos (haz pruebas).

¿Qué es lo que está pasando? La razón es que en dimensiones altas, los puntos de la muestra de entrenamiento están muy lejos unos de otros, y están cerca de la frontera, incluso para tamaños de muestra relativamente grandes como n = 1000. Cuando la dimensión crece, la situación empeora exponencialmente.

En dimensiones altas, todos los conjuntos de entrenamiento factibles se distribuyen de manera rala en el espacio de entradas.

3.3 Regresión lineal en dimensión alta

Ahora intentamos algo similar con una función que es razonable aproximar con una función lineal:

fun_cuad <- function(x)  0.5 * (1 + x[1])^2

Y queremos predecir para $x=(0,0,\ldots,0)$, cuyo valor exacto es

fun_cuad(0)

## [1] 0.5

Los datos se generan de la siguiente forma:

simular_datos <- function(p = 40){
    x <- map(1:1000,  ~ runif(p, -1, 1))
    dat <- tibble(x = x) %>% mutate(y = map_dbl(x, fun_cuad)) 
    dat
}

Por ejemplo para dimensión baja $p=1$ (nótese que una aproximación lineal es razonable):

ejemplo <- simular_datos(p = 1) %>% mutate(x = unlist(x))
ggplot(ejemplo, aes(x = x, y = y)) + geom_point() +
    geom_smooth(method = "lm")

## `geom_smooth()` using formula 'y ~ x'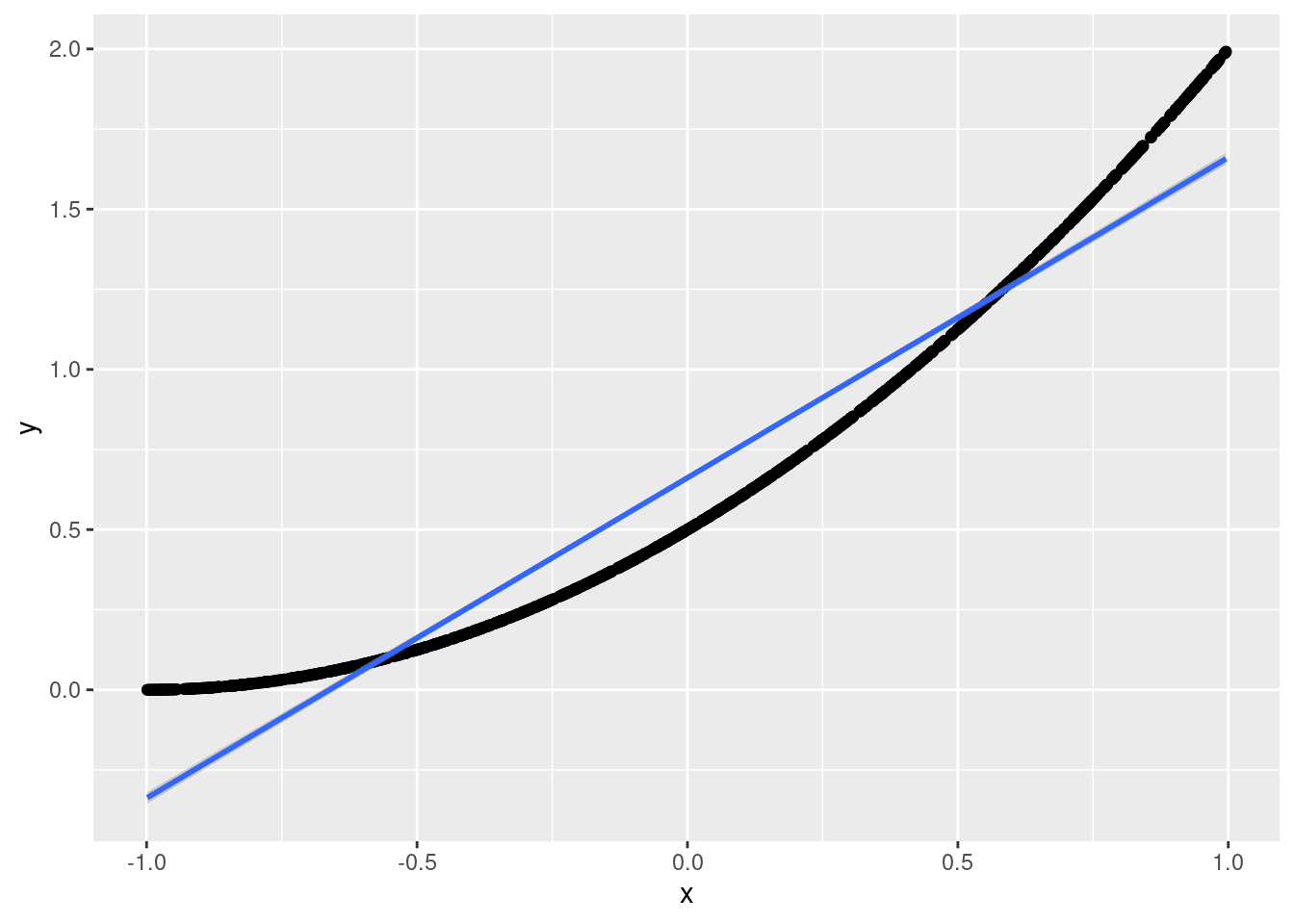

Ahora repetimos el proceso en dimensión $p=40$: simulamos las entradas, y aplicamos un vecino más cercano

vmc_1 <- function(dat){
    dat <- dat %>% 
        mutate(dist_origen = map_dbl(x, ~ sqrt(sum(.x^2)))) %>% 
        arrange(dist_origen)
        mas_cercano <- dat[1, ]
        mas_cercano$y
}
set.seed(834)
dat <- simular_datos(p = 40)
vmc_1(dat)

## [1] 1.206478

Este no es un resultado muy bueno. Sin embargo, regresión se desempeña considerablemente mejor:

regresion_pred <- function(dat){
    p <- length(dat$x[[1]])
    dat_reg <- cbind(
        y = dat$y, 
        x = matrix(unlist(dat$x), ncol = p, byrow=T)) %>% 
        as.data.frame()
    mod_lineal <- lm(y ~ ., dat = dat_reg)
    origen <- data.frame(matrix(rep(0, p), 1, p))
    names(origen) <- names(dat_reg)[2:(p+1)]
    predict(mod_lineal, newdata = origen)
}
regresion_pred(dat)

##         1 
## 0.6677861

Donde podemos ver que típicamente la predicción de regresión es mucho mejor que la de 1 vecino más cercano. Esto es porque el modelo explota la estructura aproximadamente lineal del problema (¿cuál estructura lineal? haz algunas gráficas). Nota: corre este ejemplo varias veces con semilla diferente.

Solución: vamos a hacer varias simulaciones, para ver qué modelo se desempeña mejor.

sims <- map(1:200, function(i){
    dat <- simular_datos(p = 40)
    vmc_y <- vmc_1(dat)
    reg_y <- regresion_pred(dat)
    tibble(rep = i, 
           error = c(abs(vmc_y - 0.5), abs(reg_y - 0.5)), 
            tipo = c("vmc", "regresion"))
}) %>% bind_rows
ggplot(sims, aes(x = tipo, y = error)) + geom_boxplot()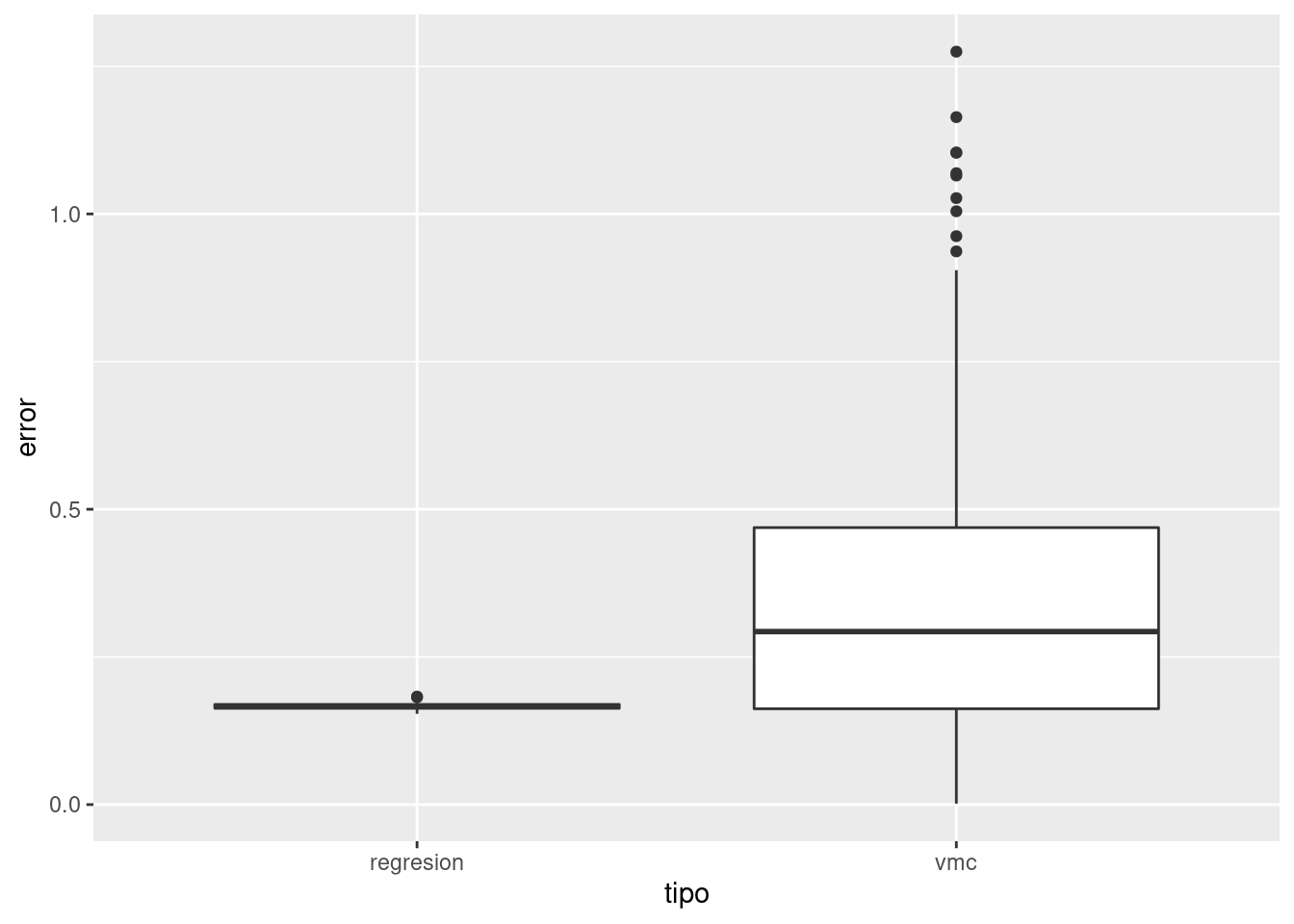

Así que típicamente el error de vecinos más cercanos es más alto que el de regresión. El error esperado es para vmc es más de doble que el de regresión:

sims %>% group_by(tipo) %>% 
    summarise(media_error = mean(error))

## `summarise()` ungrouping output (override with `.groups` argument)

## # A tibble: 2 x 2
##   tipo      media_error
##   <chr>           <dbl>
## 1 regresion       0.166
## 2 vmc             0.354

Lo que sucede más específicamente es que en regresión lineal utilizamos todos los datos para hacer nuestra estimación en cada predicción. Si la estructura del problema es aproximadamente lineal, entonces regresión lineal explota la estructura para hacer pooling de toda la información para construir predicción con sesgo y varianza bajas. En contraste, vecinos más cercanos sufre de varianza alta.

Métodos locales muchas veces no funcionan bien en dimensión alta. La razón es que:

El sesgo es alto, pues promediamos puntos muy lejanos al lugar donde queremos predecir (aunque tomemos pocos vecinos cercanos).
En el caso de que encontremos unos pocos puntos cercanos, la varianza también puede ser alta porque promediamos relativamente pocos vecinons.

Métodos con más estructura global, apropiada para el problema, logran explotar apropiadamente información de puntos que no están tan cerca del lugar donde queremos predecir.

Muchas veces el éxito en la predicción depende de establecer esas estructuras apropiadas (por ejemplo, efectos lineales cuando variables tienen efectos aproximadamente lineales, árboles cuando hay algunas interacciones, redes convolucionales para procesamiento de imágenes y señales, dependencia del contexto inmediato en modelos de lenguaje, etc.)