Clase 6 Regularizacion
Los métodos para ajustar modelos lineales que vimos en secciones anteriores (mínimos cuadrados y minimización de devianza) tienen la vulnerabilidad de que no tienen mecanismos para evitar sobreajustar los datos: queremos minimizar la devianza de prueba (o de datos futuros), e intentamos lograr eso minimizando la devianza de entrenamiento.
En esta parte veremos una de las técnicas más comunes y poderosas para evitar ese sobreajuste: la regularización. Consiste en cambiar la función objetivo que queremos minimizar por otra que penaliza modelos demasiado complejos o inverosímiles.
Así por ejemplo, en un problema de regresión, en lugar de obtener nuestro estimadores resolviendo \[\hat{\beta} = {\textrm{argmin}}_\beta D(\beta)\] donde \(D(\beta)\) es la devianza de entrenamiento,buscamos minimizar una función objetivo modificada
\[\hat{\beta} = {\textrm{argmin}}_\beta \{D(\beta) + \Omega(\beta)\}\] donde \(\Omega(\beta)\) puede ser grande para algunas configuraciones de los parámetros que son “poco verosímiles”. Este cambio evita que el proceso de minimización sobrajuste los datos haciendo \(D(\beta)\) demasiado chico.
6.0.1 Sesgo y varianza en modelos lineales
Aunque típicamente pensamos que los modelos lineales son métodos simples, con estructura rígida, y que tienden a sufrir más por sesgo que por varianza (parte de la razón por la que existen métodos más flexibles como bosques aleatorios, redes nueronales, etc.), hay varias razones por las que los métodos lineales pueden sufrir de varianza alta:
Cuando la muestra de entrenamiento es relativamente chica (\(n\) chica), la varianza puede ser alta.
Cuando el número de entradas \(p\) es grande, podemos también sufrir de varianza grande (pues tenemos muchos parámetros para estimar).
Cuando hay variables correlacionadas en las entradas la varianza también puede ser alta.
En estos casos, conviene buscar maneras de reducir varianza, generalmente a costa de un incremento de sesgo.
Ejemplo
Consideramos regresión logística. En primer lugar, supondremos que tenemos un problema con \(n=400\) y \(p=100\), y tomamos como modelo para los datos (sin ordenada al origen):
\[p_1(x)=h\left(\sum_{j=1}^{100} \beta_j x_j\right ),\]
donde \(h\) es la función logística. Nótese que este es el verdadero modelo para los datos. Para producir datos de entrenamiento, primero generamos las betas fijas, y después, utilizando estas betas, generamos 400 casos de entrenamiento.
Generamos las betas:
h <- function(x){ 1 / (1 + exp(-x))}
set.seed(2805)
beta_vec <- rnorm(100,0,0.1)
beta <- tibble(term = paste0('V', 1:length(beta_vec)), valor = beta_vec)
head(beta)## # A tibble: 6 x 2
## term valor
## <chr> <dbl>
## 1 V1 -0.120
## 2 V2 0.0346
## 3 V3 -0.0818
## 4 V4 0.0149
## 5 V5 0.0402
## 6 V6 0.00204Con esta función simulamos datos de entrenamiento (400) y datos de prueba (5000).
sim_datos <- function(n, beta){
p <- nrow(beta)
mat_x <- matrix(rnorm(n * p, 0, 0.5), n, p) + rnorm(n)
colnames(mat_x) <- beta %>% pull(term)
beta_vec <- beta %>% pull(valor)
prob <- h(mat_x %*% beta_vec)
y <- rbinom(n, 1, prob)
datos <- as_tibble(mat_x) %>%
mutate(y = factor(y, levels = c(1, 0)), prob = prob)
datos
}
set.seed(9921)
datos <- sim_datos(n = 4000, beta = beta)Y ahora separamos entrenamiento y prueba, y ajustamos el modelo de regresión logística:
## ── Attaching packages ──────────────────────────────────────────────────────────── tidymodels 0.1.1 ──## ✓ broom 0.7.0 ✓ recipes 0.1.13
## ✓ dials 0.0.8 ✓ rsample 0.0.7
## ✓ infer 0.5.3 ✓ tune 0.1.1
## ✓ modeldata 0.0.2 ✓ workflows 0.1.3
## ✓ parsnip 0.1.4 ✓ yardstick 0.0.7## Warning: package 'parsnip' was built under R version 4.0.3## ── Conflicts ─────────────────────────────────────────────────────────────── tidymodels_conflicts() ──
## x scales::discard() masks purrr::discard()
## x dplyr::filter() masks stats::filter()
## x recipes::fixed() masks stringr::fixed()
## x dplyr::lag() masks stats::lag()
## x yardstick::spec() masks readr::spec()
## x recipes::step() masks stats::step()separacion <- initial_split(datos, 0.10)
dat_ent <- training(separacion)
modelo <- logistic_reg() %>% set_engine("glm")
receta <- recipe(y ~ ., dat_ent) %>%
update_role(prob, new_role = "otras")
flujo <- workflow() %>%
add_model(modelo) %>%
add_recipe(receta)
mod_1 <- fit(flujo, dat_ent) %>% pull_workflow_fit()¿Qué tan buenas fueron nuestras estimaciones de los coeficientes verdaderos?
## Joining, by = "term"ggplot(coefs_1 %>% filter(term != "(Intercept)"),
aes(x = valor, y = estimate)) +
geom_point() +
xlab('Coeficientes') +
ylab('Coeficientes estimados') +
geom_abline() +
xlim(c(-1.5,1.5))+ ylim(c(-1.5,1.5))
Y notamos que las estimaciones no son buenas. Podemos hacer otra simulación para confirmar que el problema es que las estimaciones son muy variables.
Con otra muestra de entrenamiento, vemos que las estimaciones tienen varianza alta.
datos_ent_2 <- sim_datos(n = 400, beta = beta)
mod_2 <- fit(flujo, datos_ent_2) %>% pull_workflow_fit()
coefs_2 <- tidy(mod_2)
qplot(coefs_1$estimate, coefs_2$estimate) + xlab('Coeficientes mod 1') +
ylab('Coeficientes mod 2') +
geom_abline(intercept=0, slope =1) +
xlim(c(-1.5,1.5))+ ylim(c(-1.5,1.5))
Si repetimos varias veces:
dat_sim <- map(1:50, function(i){
datos_ent <- sim_datos(n = 400, beta = beta)
mod <- fit(flujo, datos_ent) %>% pull_workflow_fit()
tidy(mod) %>% mutate(rep = i)
}) %>% bind_rows
head(dat_sim)## # A tibble: 6 x 6
## term estimate std.error statistic p.value rep
## <chr> <dbl> <dbl> <dbl> <dbl> <int>
## 1 (Intercept) 0.0302 0.164 0.184 0.854 1
## 2 V1 -0.102 0.327 -0.313 0.755 1
## 3 V2 -0.323 0.346 -0.934 0.350 1
## 4 V3 0.677 0.328 2.07 0.0388 1
## 5 V4 0.0612 0.321 0.191 0.849 1
## 6 V5 -0.173 0.312 -0.554 0.580 1Vemos que hay mucha variabilidad en la estimación de los coeficientes (en rojo están los verdaderos):
ggplot(dat_sim, aes(x = term, y = estimate)) + geom_boxplot() +
geom_line(data = beta, aes(y = valor), group = 1, colour = "red") + coord_flip()
En la práctica, nosotros tenemos una sola muestra de entrenamiento. Así que, con una muestra de tamaño \(n=400\) como en este ejemplo, obtendremos típicamente resultados no muy buenos. Estos coeficientes ruidosos afectan nuestras predicciones de manera negativa.
Vemos ahora lo que pasa con nuestra \(\hat{p}_1(x)\) estimadas, comparándolas con \(p_1(x)\), para la primera simulación:
dat_pr <- testing(separacion)
p_entrena <- predict(mod_1, dat_ent, type = "prob") %>%
bind_cols(dat_ent %>% select(prob, y))
p_prueba <- predict(mod_1, dat_pr, type = "prob") %>%
bind_cols(dat_pr %>% select(prob, y))Para los datos de entrenamiento:
ggplot(p_entrena, aes(x = .pred_1, y = prob, colour = y)) +
geom_point() +
xlab("Predicción") + ylab("Probabilidad verdadera")
Notamos en esta gráfica:
- El ajuste parece discriminar razonablemente bien entre las dos clases del conjunto de entrenamiento (cuando la probabilidad estimada es chica, observamos casi todos clase 0, y cuando la probabilidad estimada es grande, observamos casi todos clase 1).
- Sin embargo, vemos que las probabilidades estimadas tienden a ser extremas: muchas veces estimamos probabilidad cercana a 0 o 1, cuando la probabilidad real no es tan extrema (por ejemplo, está entre 0.25 y 0.75).
Estos dos aspectos indican sobreajuste. Podemos verificar comparando con los resultados que obtenemos con la muestra de prueba, donde notamos una degradación grande de desempeño de entrenamiento a prueba (brecha grande):
roc_entrena <- p_entrena %>%
roc_curve(y, .pred_1) %>%
mutate(muestra = "entrena")
roc_prueba <- p_prueba %>%
roc_curve(y, .pred_1) %>%
mutate(muestra = "prueba")
roc_curvas <- bind_rows(roc_entrena, roc_prueba) %>%
mutate(tipo = "Sin regularización")
ggplot(roc_curvas, aes(x = 1 - specificity, y = sensitivity, colour = muestra)) +
geom_path() +
geom_abline()
Finalmente, podemos también repetir la gráfica de arriba con los datos de prueba:
ggplot(p_prueba, aes(x=.pred_1)) +
geom_point(aes(y=prob, colour=y)) +
xlab("Predicción") + ylab("Probabilidad verdadera")
Si la estimación fuera perfecta, esta gráfica sería una diagonal. Vemos entonces que
- Cometemos errores grandes en la estimación de probabilidades.
- El desempeño predictivo del modelo es pobre, aún cuando nuestro modelo puede discriminar razonablemente bien las dos clases en el conjunto de entrenamiento.
El problema no es que nuestro modelo no sea apropiado (logístico), pues ese es el modelo verdadero. El problema es el sobreajuste asociado a la variabilidad de los coeficientes que notamos arriba.
6.0.2 Reduciendo varianza de los coeficientes
Como el problema es la variabilidad de los coeficientes (no hay sesgo pues conocemos el modelo verdadero), podemos atacar este problema poniendo restricciones a los coeficientes, de manera que caigan en rangos más aceptables. Una manera de hacer esto es sustituir el problema de minimización de regresión logística, que es minimizar la devianza:
\[\min_{\beta} D(\beta)\]
con un problema penalizado
\[\min_{\beta} D(\beta) + \lambda\sum_{i=1}^p \beta_j^2\]
escogiendo un valor apropiado de \(\lambda\).
Si escogemos un valor relativamente grande de \(\lambda\), entonces terminaremos con una solución donde los coeficientes \(\beta_j\) no pueden alejarse mucho de 0, y esto previene parte del sobreajuste que observamos en nuestro primer ajuste. Otra manera de decir esto es: intentamos minimizar la devianza, pero no permitimos que los coeficientes se alejen demasiado de cero.
También es posible poner restricciones sobre el tamaño de \(\sum_{i=1}^p \beta_j^2\), lo cual es equivalente al problema de penalización.
En este caso obtenemos (veremos más del paquete glmnet):
modelo_reg <- logistic_reg(mixture = 0, penalty = 0.1) %>%
set_engine("glmnet")
flujo_reg <- workflow() %>%
add_model(modelo_reg) %>%
add_recipe(receta)
flujo_reg <- fit(flujo_reg, dat_ent)
mod_reg <- flujo_reg %>% pull_workflow_fit()## # A tibble: 101 x 3
## term estimate penalty
## <chr> <dbl> <dbl>
## 1 (Intercept) 0.0644 0.1
## 2 V1 -0.0369 0.1
## 3 V2 -0.0146 0.1
## 4 V3 -0.0139 0.1
## 5 V4 -0.163 0.1
## 6 V5 0.0947 0.1
## 7 V6 -0.0362 0.1
## 8 V7 0.0156 0.1
## 9 V8 -0.0500 0.1
## 10 V9 0.0506 0.1
## # … with 91 more rowsY podemos ver que el tamaño de los coeficientes se redujo considerablemente:
## [1] 0.4498284## [1] 15.91738Los nuevos coeficientes estimados tienen menor variación:
qplot(coefs_1$estimate, coefs_penalizado$estimate) +
xlab('Coeficientes') +
ylab('Coeficientes estimados') +
geom_abline()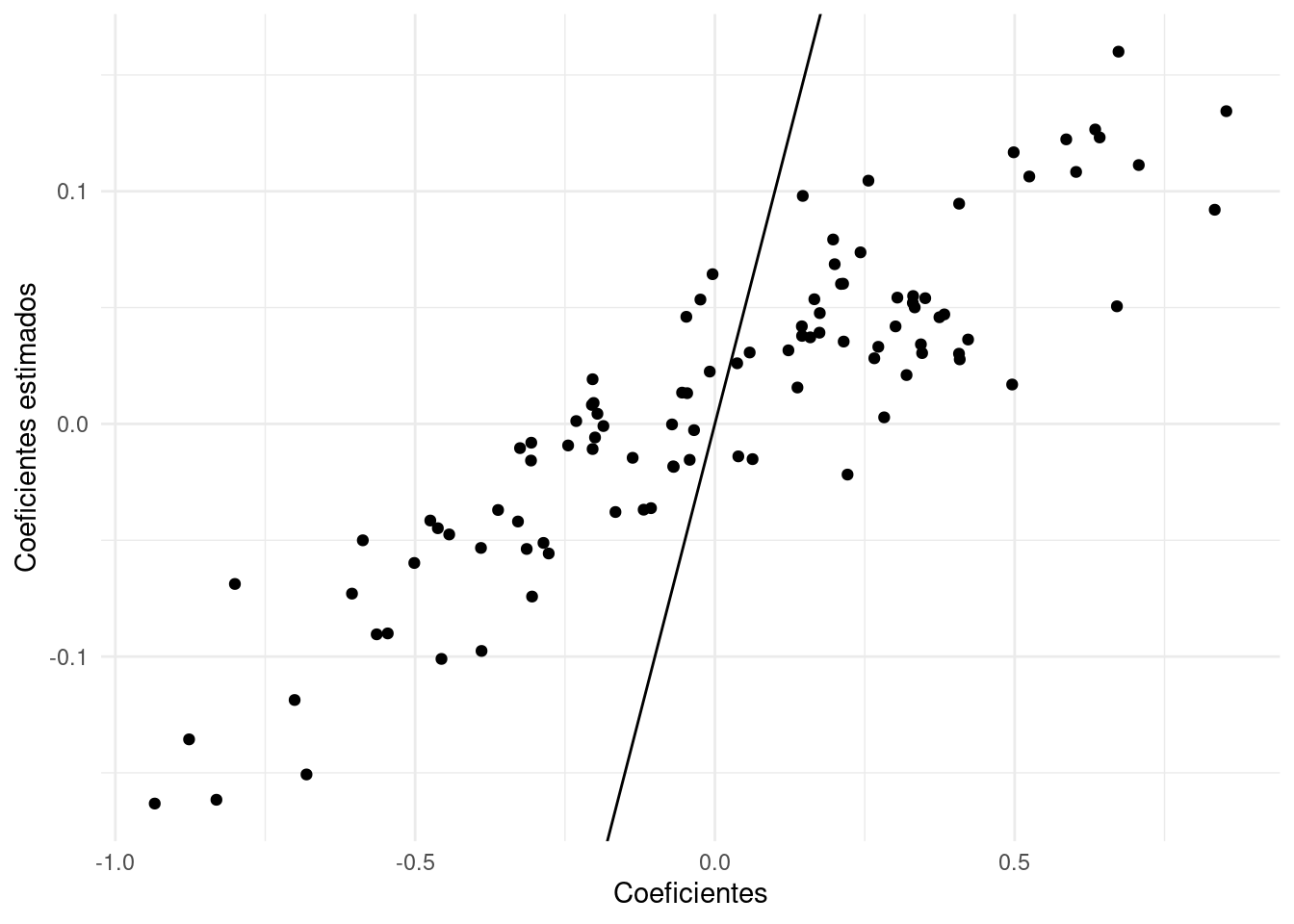
Y las probabilidades estimadas son más cercanas a las reales (recuerda que las probabilidades reales no las observamos, sólo observamos la clase):
p_entrena_reg <- predict(flujo_reg, dat_ent, type = "prob") %>%
bind_cols(dat_ent %>% select(prob, y))
ggplot(p_entrena_reg, aes(x = .pred_1, y = prob, colour = y)) +
geom_point() 
El desempeño es considerablemente mejor:
roc_entrena_reg <- predict(flujo_reg, dat_ent, type = "prob") %>%
bind_cols(dat_ent %>% select(prob, y)) %>%
roc_curve(y, .pred_1) %>%
mutate(muestra = "entrena") %>%
mutate(tipo = "Regularizado")
roc_curvas_reg <- predict(flujo_reg, dat_pr, type = "prob") %>%
bind_cols(dat_pr %>% select(prob, y)) %>%
roc_curve(y, .pred_1) %>%
mutate(muestra = "prueba") %>%
mutate(tipo = "Regularizado") %>%
bind_rows(roc_curvas, roc_entrena_reg)
roc_prueba_curvas <- roc_curvas_reg %>% filter(muestra == "prueba")
ggplot(roc_prueba_curvas,
aes(x = 1 - specificity, y = sensitivity, colour = tipo)) +
geom_path() +
geom_abline() +
labs(subtitle = "Evaluación en muestra de prueba")
Observación: Sin embargo, vemos que en la muestra de entrenamiento se desempeña mejor el modelo sin penalización, como es de esperarse (el mínimo irrestricto es más bajo que el mínimo del problema con restricción):
ggplot(roc_curvas_reg,
aes(x = 1 - specificity, y = sensitivity, colour = tipo)) +
facet_wrap(~muestra) +
geom_path() +
geom_abline()
6.1 Regularización ridge
Arriba vimos un ejemplo de regresión penalizada tipo ridge. Recordemos que para regresión lineal, buscábamos minimizar la cantidad \[D(\beta)=\frac{1}{n}\sum_{i=1}^n (y_i -\beta_0 - \sum_{j=1}^p \beta_j x_{ij})^2\] y en regresión logística, \[D(\beta)=-\frac{2}{n}\sum_{i=1}^n y_i \log(h(\beta_0 + \sum_{j=1}^p \beta_j x_{ij})) + (1-y_i) \log(1 - h(\beta_0 + \sum_{j=1}^p \beta_j x_{ij})) ,\] donde los denotamos de la misma forma para unificar notación.
Observaciones
- La idea de regresión penalizada consiste en estabilizar la estimación de los coeficientes, especialmente en casos donde tenemos muchas variables en relación a los casos de entrenamiento. La penalización no permite que varíen tan fuertemente los coeficientes.
- Cuando \(\lambda\) es mas grande, los coeficientes se encogen más fuertemente hacia cero con respecto al problema no regularizado. En este caso, estamos reduciendo la varianza pero potencialmente incrementando el sesgo.
- Cuando \(\lambda\) es mas chico, los coeficientes se encogen menos fuertemente hacia cero, y quedan más cercanos a los coeficientes de mínimos cuadrados/máxima verosimilitud. En este caso, estamos reduciendo el sesgo pero incrementando la varianza.
- Nótese que no penalizamos \(\beta_0\). Es posible hacerlo, pero típicamente no lo hacemos. En regresión lineal, de esta forma garantizamos que la predicción \(\hat{y}\), cuando todas las variables \(x_j\) toman su valor en la media, es el promedio de las \(y_i\)’s de entrenamiento. Igualmente en regresión logística, la probabilidad ajustada cuando las entradas toman su valor en la media es igual a \(h(\beta_0)\).
- Que las variables estén estandarizadas es importante para que tenga sentido la penalización. Si las variables \(x_j\) están en distintas escalas (por ejemplo pesos y dólares), entonces también los coeficientes \(\beta_j\) están en distintas escalas, y una penalización fija no afecta de la misma forma a cada coeficiente.
Resolver este problema penalizado por descenso en gradiente no tienen dificultad, pues:
De forma que sólo hay que hacer una modificación mínima al algoritmo de descenso en gradiente para el caso no regularizado.
Variables correlacionadas
Ridge es efectivo para reducir varianza inducida por variables correlacionadas. Consideramos el siguiente ejemplo donde queremos predecir el porcentaje de grasa corporal a partir de varias medidas del cuerpo (estas medidas están claramente correlacionadas):
## Parsed with column specification:
## cols(
## grasacorp = col_double(),
## edad = col_double(),
## peso = col_double(),
## estatura = col_double(),
## cuello = col_double(),
## pecho = col_double(),
## abdomen = col_double(),
## cadera = col_double(),
## muslo = col_double(),
## rodilla = col_double(),
## tobillo = col_double(),
## biceps = col_double(),
## antebrazo = col_double(),
## muñeca = col_double()
## )set.seed(831111)
grasa_particion <- initial_split(dat_grasa, 0.3)
grasa_ent <- training(grasa_particion)
grasa_pr <- testing(grasa_particion)# nota: con glmnet no es neceario normalizar, pero aquí lo hacemos
# para ver los coeficientes en términos de las variables estandarizadas:
grasa_receta <- recipe(grasacorp ~ ., grasa_ent) %>%
step_normalize(all_predictors()) %>%
prep()
modelo_1 <- linear_reg(mixture = 0) %>%
set_engine("glmnet") %>%
fit(grasacorp ~ estatura + peso + abdomen + muslo + biceps + rodilla, juice(grasa_receta))
coefs <- tidy(modelo_1$fit) %>%
filter(term != "(Intercept)")
ggplot(coefs,
aes(x = lambda, y = estimate, colour = term)) +
geom_line(size = 1.4) + scale_x_log10() +
scale_colour_manual(values = cbb_palette)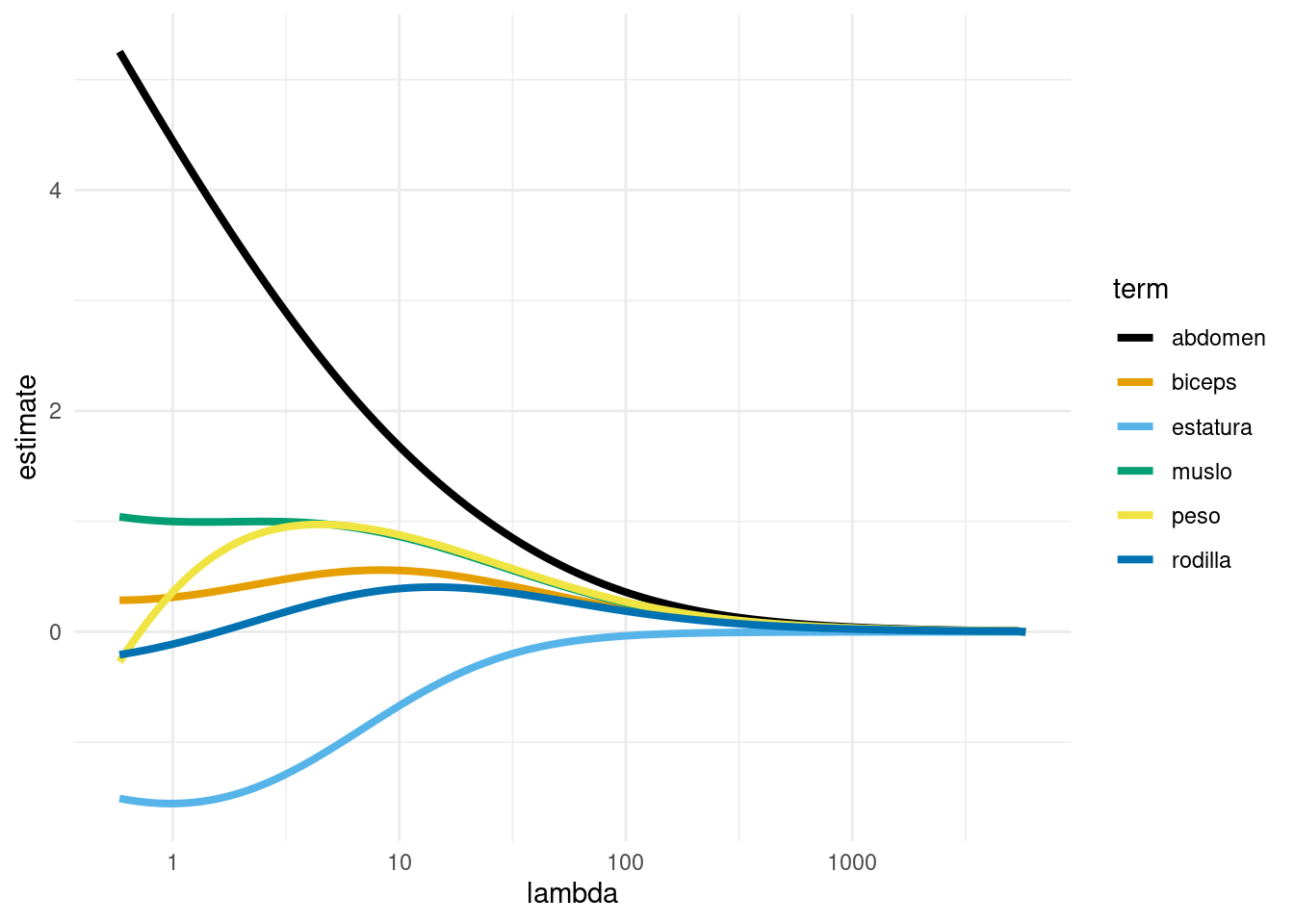
Donde notamos que las variables con correlaciones altas se “encogen” juntas hacia valores similares conforme aumentamos la constante de penalización \(\lambda\). Nótese que para regularización muy baja peso y abdomen por ejemplo, tienen signos opuestos y valores altos: esto es posible pues tienen correlación alta, de modo que la función de predicción está pobremente determinada: hay un espacio grande de pares de parámetros que dan predicciones similares, y esto resulta en coeficientes con varianza alta y predicciones inestables y ruidosas.
- Nótese, adicionalmente, que los coeficientes parecen tener más sentido en relación al problema con regularización. Regularización, en este tipo de problemas, es una de las componentes necesarias (pero no suficiente) para ir hacia interpretación del fenómeno que nos interesa.
6.1.1 Selección de coeficiente de regularización
Seleccionamos \(\lambda\) para minimizar el error de predicción, es decir, para mejorar nuestro modelo ajustado en cuanto a sus predicciones.
- No tiene sentido intentar escoger \(\lambda>0\) usando el error de entrenamiento. La razón es que siempre que aumentamos \(\lambda\), obtenemos un valor mayor de la suma de cuadrados / devianza del modelo, pues \(\lambda\) más grande implica que pesa menos la minimización de la suma de cuadrados /devianza en el problema de la minimización. En otras palabras, los coeficientes tienen una penalización más fuerte, de modo que el mínimo que se alcanza es mayor en términos de devianza.
- Intentamos escoger \(\lambda\) de forma que se minimice el error de predicción, o el error de prueba (que estima el error de predicción).
- Esto sin embargo tiene una desventaja, que es que estamos usando el conjunto de prueba repetidamente para seleccionar un modelo adecuado. Más adelante veremos una mejor manera de hacer esto
Ejemplo (simulación)
Regresamos a nuestro problema original simulado de clasificación. La función glmnet se encarga de estandarizar variables y escoger un rango adecuado de penalizaciones \(\lambda\). La función glmnet ajusta varios modelos (parámetro nlambda) para un rango amplio de penalizaciones \(\lambda\):
modelo_regularizado <- logistic_reg(mixture = 0, penalty = tune()) %>%
set_engine("glmnet")
flujo_reg <- workflow() %>%
add_model(modelo_regularizado) %>%
add_recipe(receta)glmnet_set <- parameters(penalty(range = c(-2, 3), trans = log10_trans()))
glmnet_grid <- grid_regular(glmnet_set, levels = 100)
validation_split <- validation_split(dat_ent, 0.7)
glmnet_tune <- tune_grid(flujo_reg,
resamples = validation_split,
grid = glmnet_grid,
metrics = metric_set(roc_auc, mn_log_loss))
desempeño <- glmnet_tune %>% unnest(cols = c(.metrics)) %>%
select(id, penalty, .metric, .estimate)
desempeño## # A tibble: 200 x 4
## id penalty .metric .estimate
## <chr> <dbl> <chr> <dbl>
## 1 validation 0.01 roc_auc 0.678
## 2 validation 0.0112 roc_auc 0.678
## 3 validation 0.0126 roc_auc 0.678
## 4 validation 0.0142 roc_auc 0.678
## 5 validation 0.0159 roc_auc 0.678
## 6 validation 0.0179 roc_auc 0.678
## 7 validation 0.0201 roc_auc 0.678
## 8 validation 0.0226 roc_auc 0.679
## 9 validation 0.0254 roc_auc 0.685
## 10 validation 0.0285 roc_auc 0.689
## # … with 190 more rowsggplot(desempeño %>% filter(.metric == "mn_log_loss"),
aes(x = penalty, y = .estimate)) +
geom_line() + geom_point() +
scale_x_log10() + ylab("Pérdida logarítmica") + xlab("Penalización (lambda)")
Discusión: ¿por qué la devianza de prueba tiene esta forma, que es típica para problemas de regularización?
El modelo final queda como sigue, evaluado con la muestra de prueba:
mejor <- select_best(glmnet_tune, metric = "mn_log_loss")
modelo_final <- flujo_reg %>%
finalize_workflow(mejor) %>%
fit(data = dat_ent)
preds_prob <- predict(modelo_final, dat_pr, type = "prob") %>%
bind_cols(dat_pr %>% select(y)) %>%
bind_cols(predict(modelo_final, dat_pr))## Truth
## Prediction 1 0
## 1 1185 510
## 0 646 1259## # A tibble: 1 x 3
## .metric .estimator .estimate
## <chr> <chr> <dbl>
## 1 mn_log_loss binary 0.5976.2 Entrenamiento, Validación y Prueba
El enfoque que vimos arriba, en donde dividemos la muestra en dos partes al azar, es la manera más fácil de seleccionar modelos. En general, el proceso es el siguiente:
- Una parte con los que ajustamos todos los modelos que nos interesa. Esta es la muestra de entrenamiento
- Una parte como muestra de prueba, con el que evaluamos el desempeño de cada modelo ajustado en la parte anterior. En este contexto, a esta muestra se le llama muestra de validación}.
- Posiblemente una muestra adicional independiente, que llamamos muestra de prueba, con la que hacemos una evaluación final del modelo seleccionado arriba. Es una buena idea apartar esta muestra si el proceso de validación incluye muchos métodos con varios parámetros afinados (como la \(\lambda\) de regresión ridge).

Cuando tenemos datos abundantes, este enfoque es el usual. Por ejemplo, podemos dividir la muestra en 50-25-25 por ciento. Ajustamos modelos con el primer 50%, evaluamos y seleccionamos con el segundo 25% y finalmente, si es necesario, evaluamos el modelo final seleccionado con la muestra final de 25%.
La razón de este proceso es que así podemos ir y venir entre entrenamiento y validación, buscando mejores enfoques y modelos, y no ponemos en riesgo la estimación final del error. (Pregunta: ¿por qué probar agresivamente buscando mejorar el error de validación podría ponder en riesgo la estimación final del error del modelo seleccionado? )
Pudes ver el ejemplo anterior donde usamos esta estrategia para evaluar distintos valores de \(\lambda\).
6.2.1 Validación cruzada
En muchos casos, no queremos apartar una muestra de validación para seleccionar modelos, pues no tenemos muchos datos (al dividir la muestra obtendríamos un modelo relativamente malo en relación al que resulta de todos los datos).
Un criterio para seleccionar la regularización adecuada es el de **validación cruzada*, que es un método computacional para producir una estimación interna (usando sólo muestra de entrenamiento) del error de predicción.
Validación cruzada también tiene nos da diagnósticos adicionales para entender la variación del desempeño según el conjunto de datos de entrenamiento que usemos, algo que es más difícil ver si solo tenemos una muestra de validación.
En validación cruzada (con \(k\) vueltas), construimos al azar una partición, con tamaños similares, de la muestra de entrenamiento \({\mathcal L}=\{ (x_i,y_i)\}_{i=1}^n\):
\[ {\mathcal L}={\mathcal L}_1\cup {\mathcal L}_2\cup\cdots\cup {\mathcal L}_k.\]

Construimos \(k\) modelos distintos, digamos \(\hat{f}_j\), usando solamente la muestra \({\mathcal L}-{\mathcal L}_j\), para \(j=1,2,\ldots, k\). Cada uno de estos modelos lo evaluamos usando la parte que no usamos para entrenarlo, \({\mathcal L}_j\), para obtener una estimación honesta del error del modelo \(\hat{f}_k\), a la que denotamos por \(\hat{e}_j\).
Notemos entonces que tenemos \(k\) estimaciones del error \(\hat{e}_1,\ldots, \hat{e}_k\), una para cada uno de los modelos que construimos. La idea ahora es que
- Cada uno de los modelos \(\hat{f}_j\) es similar al modelo ajustado con toda la muestra \(\hat{f}\), de forma que podemos pensar que cada una de las estimaciones \(\hat{e}_j\) es un estimador del error de \(\hat{f}\).
- Dado el punto anterior, podemos construir una mejor estimación promediando las \(k\) estimaciones anteriores, para obtener: \[\widehat{cv} = \frac{1}{k} \sum_{j=1}^k \hat{e}_j.\]
- ¿Cómo escoger \(k\)? Usualmente se usan \(k=5,10,20\), y \(k=10\) es el más popular. La razón es que cuando \(k\) es muy chico, tendemos a evaluar modelos construidos con pocos datos (comparado al modelo con todos los datos de entrenamiento). Por otra parte, cuando \(k\) es grande el método puede ser muy costoso (por ejemplo, si \(k=N\), hay que entrenar un modelo para cada dato de entrada).
Ejemplo
Consideremos nuestro problema de predicción de grasa corporal. Definimos el flujo de procesamiento, e indicamos qué parametros queremos afinar:
# con tune() indicamos que ese parámetro será afinado
modelo_regularizado <- linear_reg(mixture = 0, penalty = tune()) %>%
set_engine("glmnet")
flujo_reg <- workflow() %>%
add_model(modelo_regularizado) %>%
add_recipe(grasa_receta)# construimos conjunto de parámetros
bf_set <- parameters(penalty(range = c(-1, 2), trans = log10_trans()))
# construimos un grid para probar valores individuales
bf_grid <- grid_regular(bf_set, levels = 50)
bf_grid## # A tibble: 50 x 1
## penalty
## <dbl>
## 1 0.1
## 2 0.115
## 3 0.133
## 4 0.153
## 5 0.176
## 6 0.202
## 7 0.233
## 8 0.268
## 9 0.309
## 10 0.356
## # … with 40 more rowsYa hora construimos los cortes de validación cruzada. Haremos validación cruzada 10
validacion_particion <- vfold_cv(grasa_ent, v = 10)
# tiene información de índices en cada "fold" o "doblez"vuelta"
validacion_particion## # 10-fold cross-validation
## # A tibble: 10 x 2
## splits id
## <list> <chr>
## 1 <split [68/8]> Fold01
## 2 <split [68/8]> Fold02
## 3 <split [68/8]> Fold03
## 4 <split [68/8]> Fold04
## 5 <split [68/8]> Fold05
## 6 <split [68/8]> Fold06
## 7 <split [69/7]> Fold07
## 8 <split [69/7]> Fold08
## 9 <split [69/7]> Fold09
## 10 <split [69/7]> Fold10Y corremos sobre todo el grid los modelos, probando con los cortes de validación cruzada:
metricas_vc <- tune_grid(flujo_reg,
resamples = validacion_particion,
grid = bf_grid,
metrics = metric_set(rmse, mae))
metricas_vc %>% unnest(.metrics)## # A tibble: 1,000 x 8
## splits id penalty .metric .estimator .estimate .config .notes
## <list> <chr> <dbl> <chr> <chr> <dbl> <chr> <list>
## 1 <split [68/… Fold01 0.1 rmse standard 5.95 Model01 <tibble [0 …
## 2 <split [68/… Fold01 0.115 rmse standard 5.95 Model02 <tibble [0 …
## 3 <split [68/… Fold01 0.133 rmse standard 5.95 Model03 <tibble [0 …
## 4 <split [68/… Fold01 0.153 rmse standard 5.95 Model04 <tibble [0 …
## 5 <split [68/… Fold01 0.176 rmse standard 5.95 Model05 <tibble [0 …
## 6 <split [68/… Fold01 0.202 rmse standard 5.95 Model06 <tibble [0 …
## 7 <split [68/… Fold01 0.233 rmse standard 5.95 Model07 <tibble [0 …
## 8 <split [68/… Fold01 0.268 rmse standard 5.95 Model08 <tibble [0 …
## 9 <split [68/… Fold01 0.309 rmse standard 5.95 Model09 <tibble [0 …
## 10 <split [68/… Fold01 0.356 rmse standard 5.95 Model10 <tibble [0 …
## # … with 990 more rowsVemos que esta función da un valor del error para cada vuelta de validación cruzada, y cada valor de lambda que pusimos en el grid:
## # A tibble: 20 x 3
## # Groups: id, .metric [20]
## id .metric n
## <chr> <chr> <int>
## 1 Fold01 mae 50
## 2 Fold01 rmse 50
## 3 Fold02 mae 50
## 4 Fold02 rmse 50
## 5 Fold03 mae 50
## 6 Fold03 rmse 50
## 7 Fold04 mae 50
## 8 Fold04 rmse 50
## 9 Fold05 mae 50
## 10 Fold05 rmse 50
## 11 Fold06 mae 50
## 12 Fold06 rmse 50
## 13 Fold07 mae 50
## 14 Fold07 rmse 50
## 15 Fold08 mae 50
## 16 Fold08 rmse 50
## 17 Fold09 mae 50
## 18 Fold09 rmse 50
## 19 Fold10 mae 50
## 20 Fold10 rmse 50Y ahora podemos graficar:
ggplot(metricas_vc %>% unnest(.metrics) %>% filter(.metric == "mae"),
aes(x = penalty, y = .estimate)) + geom_point() +
scale_x_log10()
Nótese que para valores bajos de penalización hay variación considerable en el error (los modelos cambian mucho de corrida a corrida). Para resumir, como explicamos arriba, podemos resumir con media y error estándar:
## # A tibble: 100 x 7
## penalty .metric .estimator mean n std_err .config
## <dbl> <chr> <chr> <dbl> <int> <dbl> <chr>
## 1 0.1 mae standard 4.00 10 0.323 Model01
## 2 0.1 rmse standard 4.64 10 0.302 Model01
## 3 0.115 mae standard 4.00 10 0.323 Model02
## 4 0.115 rmse standard 4.64 10 0.302 Model02
## 5 0.133 mae standard 4.00 10 0.323 Model03
## 6 0.133 rmse standard 4.64 10 0.302 Model03
## 7 0.153 mae standard 4.00 10 0.323 Model04
## 8 0.153 rmse standard 4.64 10 0.302 Model04
## 9 0.176 mae standard 4.00 10 0.323 Model05
## 10 0.176 rmse standard 4.64 10 0.302 Model05
## # … with 90 more rowsg_1 <- ggplot(metricas_resumen %>% filter(.metric == "mae"),
aes(x = penalty, y = mean, ymin = mean - std_err, ymax = mean + std_err)) +
geom_linerange() +
geom_point(colour = "red") +
scale_x_log10()
g_1
Nótese que la estimación del error de predicción por validación cruzada incluye un error de estimación (intervalos). Esto nos da dos opciones para escoger la lambda final:
- Escoger la que de el mínimo valor de error por validación cruzada
- Escoger la lambda más grande que no esté a más de 1 error estándar del mínimo.
Podemos obtener estos resultados de esta forma:
## # A tibble: 5 x 7
## penalty .metric .estimator mean n std_err .config
## <dbl> <chr> <chr> <dbl> <int> <dbl> <chr>
## 1 0.1 mae standard 4.00 10 0.323 Model01
## 2 0.115 mae standard 4.00 10 0.323 Model02
## 3 0.133 mae standard 4.00 10 0.323 Model03
## 4 0.153 mae standard 4.00 10 0.323 Model04
## 5 0.176 mae standard 4.00 10 0.323 Model05minimo <- metricas_vc %>% select_best(metric = "mae")
minimo_ee <- metricas_vc %>% select_by_one_std_err(metric = "mae", desc(penalty))En la gráfica se muestran las dos posiblidades:
g_1 +
geom_vline(data= minimo, aes(xintercept = penalty), colour = "blue") +
geom_vline(data = minimo_ee, aes(xintercept = penalty), colour = "blue")
6.2.2 ¿Cómo se desempeña validación cruzada como estimación del error?
Podemos comparar el desempeño estimado con validación cruzada con el de muestra de prueba: Consideremos nuestro ejemplo simulado de regresión logística. Repetiremos varias veces el ajuste y compararemos el error de prueba con el estimado por validación cruzada:
simular_evals <- function(rep, flujo){
datos <- sim_datos(n = 1000, beta = beta[1:20, ])
particion <- initial_split(datos, 0.2)
datos_ent <- training(particion)
datos_pr <- testing(particion)
modelo_1 <- logistic_reg(penalty = 0.1) %>%
set_engine("glmnet")
flujo_1 <- workflow() %>%
add_model(modelo_1) %>%
add_formula(y ~ .)
# evaluar con muestra de prueba
metricas <- metric_set(mn_log_loss, roc_auc)
flujo_ajustado <- flujo_1 %>% fit(datos_ent)
eval_prueba <- predict(flujo_ajustado, datos_pr, type = "prob") %>%
bind_cols(datos_pr %>% select(y)) %>%
metricas(y, .pred_1)
# particionar para validación cruzada
particiones_val_cruzada <- vfold_cv(datos_ent, v = 10)
eval_vc <- flujo_1 %>%
fit_resamples(resamples = particiones_val_cruzada, metrics = metricas) %>%
collect_metrics()
res_tbl <-
eval_prueba %>% mutate(tipo = "prueba") %>%
bind_rows(eval_vc %>%
select(.metric, .estimator, .estimate = mean) %>%
mutate(tipo = "val_cruzada"))
}
evals_tbl <- tibble(rep = 1:50) %>%
mutate(data = map(rep, ~ simular_evals(.x, flujo_1))) %>%
unnest(data)ggplot(evals_tbl %>%
filter(.metric == "mn_log_loss") %>%
pivot_wider(names_from = tipo, values_from = .estimate),
aes(x = prueba, y = val_cruzada)) +
geom_point() + facet_wrap(~ .metric) +
geom_abline(colour = "red") + xlim(c(0.65,0.75)) + ylim(c(0.65,0.75))
Observa los rangos de los ejes. Vemos que aunque los dos tipos de estimaciones están centradas en lugares similares, el error por validación cruzada es ligeramente pesimista (como esperábamos), y no está muy correlacionado con el error de prueba.
Sin embargo, cuando usamos validación cruzada para seleccionar modelos tenemos lo siguiente:
set.seed(8559)
datos <- sim_datos(n = 1000, beta = beta[1:50, ])
modelo <- logistic_reg(mixture = 0, penalty = tune()) %>%
set_engine("glmnet")
flujo <- workflow() %>%
add_model(modelo) %>%
add_formula(y ~ .)
# crear partición de análisis y evaluación
particion_val <- validation_split(datos, 0.5)
candidatos <- tibble(penalty = exp(seq(-5, 5, 1)))
# evaluar
val_datos <- tune_grid(flujo, resamples = particion_val, grid = candidatos,
metrics = metric_set(mn_log_loss, roc_auc)) %>%
collect_metrics() %>%
select(penalty, .metric, mean) %>%
mutate(tipo ="datos de validación")# extraer datos de entrenamiento
datos_ent <- analysis(particion_val$splits[[1]])
particion_vc <- vfold_cv(datos_ent, v = 10)
val_cruzada <- tune_grid(flujo, resamples = particion_vc, grid = candidatos,
metrics = metric_set(mn_log_loss, roc_auc)) %>%
collect_metrics() %>%
select(penalty, .metric, mean) %>%
mutate(tipo = "validación cruzada")comparacion_val <- bind_rows(val_datos, val_cruzada) %>%
filter(.metric == "mn_log_loss")
ggplot(comparacion_val, aes(x = penalty, y = mean, colour = tipo)) +
geom_line() + geom_point() +
facet_wrap(~.metric) +
scale_x_log10()
Vemos que la estimación en algunos casos no es tan buena, aún cuando todos los datos fueron usados. Pero el mínimo se encuentra en lugares muy similares. La razón es:
Validación cruzada en realidad considera perturbaciones del conjunto de entrenamiento, de forma que lo que intenta evaluar es el error producido, para cada lambda, sobre distintas muestras de entrenamiento.
En realidad nosotros queremos evaluar el error de predicción del modelo que ajustamos. Validación cruzada es más un estimador del error esperado de predicción sobre los modelos que ajustaríamos con distintas muestras de entrenamiento.El resultado es que:
- Usamos validación cruzada para escoger la complejidad adecuada de la familia de modelos que consideramos.
- Como estimación del error de predicción del modelo que ajustamos, validación cruzada es más seguro que usar el error de entrenamiento, que muchas veces puede estar fuertemente sesgado hacia abajo. Sin embargo, lo mejor en este caso es utilizar una muestra de prueba.
Ejercicio
Consideremos el ejemplo de reconocimiento de dígitos y regresión logística multinomial. Vimos que obtuvimos mejores resultados detendiéndonos prematuramente en el ajuste que minimizando el error de entrenamiento.
La razón es que usamos descenso en gradiente comenzando con coeficientes en 0. Si hacemos iteraciones, nos movemos en dirección del mínimo sin alejarnos mucho del origen, y esto resulta ser una forma de regularización: los coeficientes están “encogidos” hacia el origen. Esta es una manera de regularizar, y se llama normalmente early stopping.
Podemos también hacer regresión ridge para el problema de los dígitos.
digitos_entrena <- read_csv('../datos/zip-train.csv')
digitos_prueba <- read_csv('../datos/zip-test.csv')
names(digitos_entrena)[1] <- 'digito'
names(digitos_entrena)[2:257] <- paste0('pixel_', 1:256)
names(digitos_prueba)[1] <- 'digito'
names(digitos_prueba)[2:257] <- paste0('pixel_', 1:256)
digitos_entrena <- digitos_entrena %>%
mutate(digito = factor(digito, levels = seq(0, 9, 1)))
digitos_prueba <- digitos_prueba %>%
mutate(digito = factor(digito, levels = seq(0, 9, 1)))Vamos a correr modelos con varias lambda, y estimar su error con validación cruzada. Primero definimos el modelo y el preprocesamiento
set.seed(2912)
if(TRUE){
digitos_entrena_s <- sample_n(digitos_entrena, size = 2000)
} else {
digitos_entrena_s <- digitos_entrena
}
modelo_digitos <- multinom_reg(penalty = tune()) %>%
set_engine("keras") %>%
set_mode("classification") %>%
set_args(epochs = 5000, optimizer = keras::optimizer_sgd(lr = 0.2),
batch_size = nrow(digitos_entrena_s),
verbose = FALSE, hidden_units = 10)
receta_digitos <- recipe(digito ~ ., digitos_entrena_s)
flujo_digitos <- workflow() %>%
add_model(modelo_digitos) %>%
add_recipe(receta_digitos)Ahora definimos los cortes de validación cruzada y evaluamos
particion_vc <- validation_split(digitos_entrena_s, strata = digito, 0.9)
grid_lambda <- tibble(penalty = exp(c(-10, -5, -4, -3, -2)))
res_val <- tune_grid(
flujo_digitos,
resamples = particion_vc,
grid = grid_lambda,
metrics = metric_set(mn_log_loss))
res_val %>% collect_metrics()## # A tibble: 5 x 7
## penalty .metric .estimator mean n std_err .config
## <dbl> <chr> <chr> <dbl> <int> <dbl> <chr>
## 1 0.0000454 mn_log_loss multiclass 0.302 1 NA Model1
## 2 0.00674 mn_log_loss multiclass 0.230 1 NA Model2
## 3 0.0183 mn_log_loss multiclass 0.252 1 NA Model3
## 4 0.0498 mn_log_loss multiclass 0.289 1 NA Model4
## 5 0.135 mn_log_loss multiclass 0.474 1 NA Model5Ahora hacemos predicciones para el conjunto de prueba, usando la lambda que nos dio el menor error de validación cruzada:
mejor <- select_best(res_val, metric = "mn_log_loss")
modelo_final <-
flujo_digitos %>%
finalize_workflow(mejor) %>%
fit(data = digitos_entrena_s)
digitos_pr <- bake(modelo_final %>% pull_workflow_prepped_recipe, digitos_prueba)
predict(modelo_final, digitos_pr, type ="prob") %>%
bind_cols(digitos_pr %>% select(digito)) %>%
mn_log_loss(digito, .pred_0:.pred_9)## # A tibble: 1 x 3
## .metric .estimator .estimate
## <chr> <chr> <dbl>
## 1 mn_log_loss multiclass 0.362Y evaluamos la tasa de clasificación incorrecta:
predict(modelo_final, digitos_pr) %>%
bind_cols(digitos_pr %>% select(digito)) %>%
accuracy(digito, .pred_class)## # A tibble: 1 x 3
## .metric .estimator .estimate
## <chr> <chr> <dbl>
## 1 accuracy multiclass 0.900Este modelo mejora considerablemente al modelo sin regularización.
Observación: Cuando vimos regresión multinomial, la última clase es uno menos la suma del resto de probabilidades de clase (\((K-1)(p+1)\) parámetros). La salida de glmnet, sin embargo, tiene coeficientes para todas las clases (\(K(p+1)\) parámetros). ¿Por qué en regresión ridge no es tan importante que el modelo esté sobreparametrizado?
6.3 Regularización lasso
Otra forma de regularización es el lasso, que en lugar de penalizar con la suma de cuadrados en los coeficientes, penaliza por la suma de su valor absoluto.
El problema de minimización de ridge y de lasso se pueden reescribir como problemas de restricción:
\(s\) y \(t\) chicas corresponden a valores de penalización \(\lambda\) grandes.
En un principio, puede parecer que ridge y lasso deben dar resultados muy similares, pues en ambos casos penalizamos por el tamaño de los coeficientes. Sin embargo, son distintos de una manera muy importante.
En la siguiente gráfica representamos las curvas de nivel de \(D(\beta)\). Recordemos que en mínimos cuadrados o regresión logística intentamos minimizar esta cantidad sin restricciones, y este mínimo se encuentra en el centro de estas curvas de nivel. Para el problema restringido, buscamos más bien la curva de nivel más baja que intersecta la restricción:
 Y obsérvese ahora que la solución de lasso puede hacer algunos coeficientes
igual a 0. Es decir,
Y obsérvese ahora que la solución de lasso puede hacer algunos coeficientes
igual a 0. Es decir,
En regresión ridge, los coeficientes se encogen gradualmente desde la solución no restringida hasta el origen. Ridge es un método de encogimiento de coeficientes.
En regresión lasso, los coeficientes se encogen gradualmente, pero también se excluyen variables del modelo. Por eso lasso es un método de encogimiento y selección de variables.- Regresión ridge es especialmente útil cuando tenemos varias variables de entrada fuertemente correlacionadas. Regresión ridge intenta encoger juntos coeficientes de variables correlacionadas para reducir varianza en las predicciones.
- Lasso encoge igualmente coeficientes para reducir varianza, pero también comparte similitudes con regresión de mejor subconjunto, en donde para cada número de variables \(l\) buscamos escoger las \(l\) variables que den el mejor modelo. Sin embargo, el enfoque de lasso es más escalable y puede calcularse de manera más simple.
- Descenso en gradiente no es apropiado para regresión lasso (ver documentación de glmnet para ver cómo se hace en este paquete). El problema es que los coeficientes nunca se hacen exactamente cero, pues la restricción no es diferenciable en el origen (coeficientes igual a cero).
Ejemplo
Consideramos el ejemplo de bodyfat:
library(readr)
dat_grasa <- read_csv(file = '../datos/bodyfat.csv')
# mixture = 1 es lasso, mixture = 0 es ridge
modelo_regularizado <- linear_reg(mixture = 1, penalty = tune()) %>%
set_engine("glmnet")
flujo_reg <- workflow() %>%
add_model(modelo_regularizado) %>%
add_recipe(grasa_receta)validacion_particion <- vfold_cv(grasa_ent, v = 10)
metricas_vc <- tune_grid(flujo_reg,
resamples = validacion_particion,
grid = bf_grid,
metrics = metric_set(rmse, mae))
metricas_resumen <- metricas_vc %>% collect_metrics()
metricas_resumen## # A tibble: 100 x 7
## penalty .metric .estimator mean n std_err .config
## <dbl> <chr> <chr> <dbl> <int> <dbl> <chr>
## 1 0.1 mae standard 3.74 10 0.298 Model01
## 2 0.1 rmse standard 4.33 10 0.248 Model01
## 3 0.115 mae standard 3.74 10 0.297 Model02
## 4 0.115 rmse standard 4.33 10 0.246 Model02
## 5 0.133 mae standard 3.74 10 0.296 Model03
## 6 0.133 rmse standard 4.33 10 0.245 Model03
## 7 0.153 mae standard 3.74 10 0.293 Model04
## 8 0.153 rmse standard 4.34 10 0.242 Model04
## 9 0.176 mae standard 3.75 10 0.289 Model05
## 10 0.176 rmse standard 4.35 10 0.240 Model05
## # … with 90 more rowsg_1 <- ggplot(metricas_resumen %>% filter(.metric == "mae"),
aes(x = penalty, y = mean, ymin = mean - std_err, ymax = mean + std_err)) +
geom_linerange() +
geom_point(colour = "red") +
scale_x_log10()
g_1
Veamos los coeficientes para un modelo regularizado con la \(\lambda\) máxima con error consistente con el mínimo (por validación cruzada):
mejor <- select_best(metricas_vc, metric = "mae", penalty)
modelo_final <-
flujo_reg %>%
finalize_workflow(mejor) %>%
fit(data = grasa_ent)
coeficientes <- modelo_final %>% pull_workflow_fit() %>% tidy
coeficientes %>% mutate(across(where(is.numeric), round, 2))## # A tibble: 14 x 3
## term estimate penalty
## <chr> <dbl> <dbl>
## 1 (Intercept) 18.4 0.13
## 2 edad 0.74 0.13
## 3 peso 0 0.13
## 4 estatura -1.08 0.13
## 5 cuello -0.14 0.13
## 6 pecho 0 0.13
## 7 abdomen 6.83 0.13
## 8 cadera 0 0.13
## 9 muslo 0.48 0.13
## 10 rodilla 0 0.13
## 11 tobillo 0 0.13
## 12 biceps 0.21 0.13
## 13 antebrazo 0.51 0.13
## 14 muñeca -2.44 0.13Y nótese que este modelo solo incluye 5 variables. El error de predicción es similar al modelo que incluye todas las variables, y terminamos con un modelo considerablemente más simple con error comparable
La traza confirma que la regularización lasso, además de encoger coeficientes, saca variables del modelo conforme el valor de regularización aumenta:
modelo_1 <- linear_reg(mixture = 1) %>%
set_engine("glmnet") %>%
fit(grasacorp ~ estatura + peso + abdomen + muslo + biceps + rodilla + edad + cuello,
grasa_ent)
coefs <- tidy(modelo_1$fit) %>%
filter(term != "(Intercept)")
ggplot(coefs,
aes(x = lambda, y = estimate, colour = term)) +
geom_line(size = 1.4) + scale_x_log10() +
scale_colour_manual(values = cbb_palette)