Clase 11 Métodos basados en árboles: boosting
Boosting también utiliza la idea de un “ensamble” de árboles. La diferencia grande con bagging y bosques aleatorios en que la sucesión de árboles de boosting se ‘adapta’ al comportamiento del predictor a lo largo de las iteraciones, haciendo reponderaciones de los datos de entrenamiento para que el algoritmo se concentre en las predicciones más pobres. Boosting generalmente funciona bien con árboles chicos (cada uno con sesgo alto), mientras que bosques aleatorios funciona con árboles grandes (sesgo bajo).
En boosting usamos muchos árboles chicos adaptados secuencialmente. La disminución del sesgo proviene de usar distintos árboles que se encargan de adaptar el predictor a distintas partes del conjunto de entrenamiento. El control de varianza se logra con tasas de aprendizaje y tamaño de árboles, como veremos más adelante.
En bosques aleatorios usamos muchos árboles grandes, cada uno con una muestra de entrenamiento perturbada (bootstrap). El control de varianza se logra promediando sobre esas muestras bootstrap de entrenamiento.
Igual que bosques aleatorios, boosting es también un método que generalmente tiene alto poder predictivo.
11.1 Forward stagewise additive modeling (FSAM)
Aunque existen versiones de boosting (Adaboost) desde los 90s, una buena manera de entender los algoritmos es mediante un proceso general de modelado por estapas (FSAM).
11.2 Discusión
Consideramos primero un problema de regresión, que queremos atacar con un predictor de la forma \[f(x) = \sum_{k=1}^m \beta_k b_k(x),\] donde los \(b_k\) son árboles. Podemos absorber el coeficiente \(\beta_k\) dentro del árbol \(b_k(x)\), y escribimos
\[f(x) = \sum_{k=1}^m T_k(x),\]
Para ajustar este tipo de modelos, buscamos minimizar la pérdida de entrenamiento:
\[\begin{equation} \min \sum_{i=1}^N L(y^{(i)}, \sum_{k=1}^M T_k(x^{(i)})) \end{equation}\]
Este puede ser un problema difícil, dependiendo de la familia que usemos para los árboles \(T_k\), y sería difícil resolver por fuerza bruta. Para resolver este problema, podemos intentar una heurística secuencial o por etapas:
Si tenemos \[f_{m-1}(x) = \sum_{k=1}^{m-1} T_k(x),\]
intentamos resolver el problema (añadir un término adicional)
\[\begin{equation} \min_{T} \sum_{i=1}^N L(y^{(i)}, f_{m-1}(x^{(i)}) + T(x^{(i)})) \end{equation}\]
Por ejemplo, para pérdida cuadrática (en regresión), buscamos resolver
\[\begin{equation} \min_{T} \sum_{i=1}^N (y^{(i)} - f_{m-1}(x^{(i)}) - T(x^{(i)}))^2 \end{equation}\]
Si ponemos \[ r_{m-1}^{(i)} = y^{(i)} - f_{m-1}(x^{(i)}),\] que es el error para el caso \(i\) bajo el modelo \(f_{m-1}\), entonces reescribimos el problema anterior como \[\begin{equation} \min_{T} \sum_{i=1}^N ( r_{m-1}^{(i)} - T(x^{(i)}))^2 \end{equation}\]
Este problema consiste en ajustar un árbol a los residuales o errores del paso anterior. Otra manera de decir esto es que añadimos un término adicional que intenta corregir los que el modelo anterior no pudo predecir bien. La idea es repetir este proceso para ir reduciendo los residuales, agregando un árbol a la vez.
11.3 Algoritmo FSAM
Esta idea es la base del siguiente algoritmo:
Algoritmo FSAM (forward stagewise additive modeling)
- Tomamos \(f_0(x)=0\)
- Para \(m=1\) hasta \(M\),
- Resolvemos \[T_m = argmin_{T} \sum_{i=1}^N L(y^{(i)}, f_{m-1}(x^{(i)}) + T(x^{(i)}))\]
- Ponemos \[f_m(x) = f_{m-1}(x) + T_m(x)\]
- Nuestro predictor final es \(f(x) = \sum_{m=1}^M T_(x)\).
Observaciones: Generalmente los árboles sobre los que optimizamos están restringidos a una familia relativamente chica: por ejemplo, árboles de profundidad no mayor a \(2,3,\ldots, 8\).
Este algoritmo se puede aplicar directamente para problemas de regresión, como vimos en la discusión anterior: simplemente hay que ajustar árboles a los residuales del modelo del paso anterior. Sin embargo, no está claro cómo aplicarlo cuando la función de pérdida no es mínimos cuadrados (por ejemplo, regresión logística).
Ejemplo (regresión)
Podemos hacer FSAM directamente sobre un problema de regresión.
set.seed(227818)
library(rpart)
x <- rnorm(200, 0, 30)
y <- 2*ifelse(x < 0, 0, sqrt(x)) + rnorm(200, 0, 0.5)
dat <- data.frame(x=x, y=y)Pondremos los árboles de cada paso en una lista. Podemos comenzar con una constante en lugar de 0.
arboles_fsam <- list()
arboles_fsam[[1]] <- rpart(y ~ x, data = dat,
control = list(maxdepth = 0))
arboles_fsam[[1]]## n= 200
##
## node), split, n, deviance, yval
## * denotes terminal node
##
## 1) root 200 5370.398 4.675925 *Ahora construirmos nuestra función de predicción y el paso que agrega un árbol
predecir_arboles <- function(arboles_fsam, x){
preds <- lapply(arboles_fsam, function(arbol){
predict(arbol, data.frame(x = x))
})
reduce(preds, `+`)
}
agregar_arbol <- function(arboles_fsam, dat, plot=TRUE){
n <- length(arboles_fsam)
preds <- predecir_arboles(arboles_fsam, x = dat$x)
dat$res <- y - preds
arboles_fsam[[n+1]] <- rpart(res ~ x, data = dat,
control = list(maxdepth = 1))
dat$preds_nuevo <- predict(arboles_fsam[[n+1]])
dat$preds <- predecir_arboles(arboles_fsam, x=dat$x)
g_res <- ggplot(dat, aes(x = x)) +
geom_point(aes(y=res), size =1.1, alpha = 0.7, colour ="red") +
geom_line(aes(y=preds_nuevo)) +
labs(title = 'Residuales') + ylim(c(-10,10))
g_agregado <- ggplot(dat, aes(x=x)) +
geom_point(aes(y = y), size = 1.1, alpha = 0.7, colour = "red") +
geom_line(aes(y=preds), colour = 'black',
size=1.1) +
labs(title ='Ajuste')
if(plot){
print(g_res)
print(g_agregado)
}
arboles_fsam
}Ahora construiremos el primer árbol. Usaremos ‘troncos’ (stumps), árboles con un solo corte: Los primeros residuales son simplemente las \(y\)’s observadas
## Warning: Removed 8 rows containing missing values (geom_point).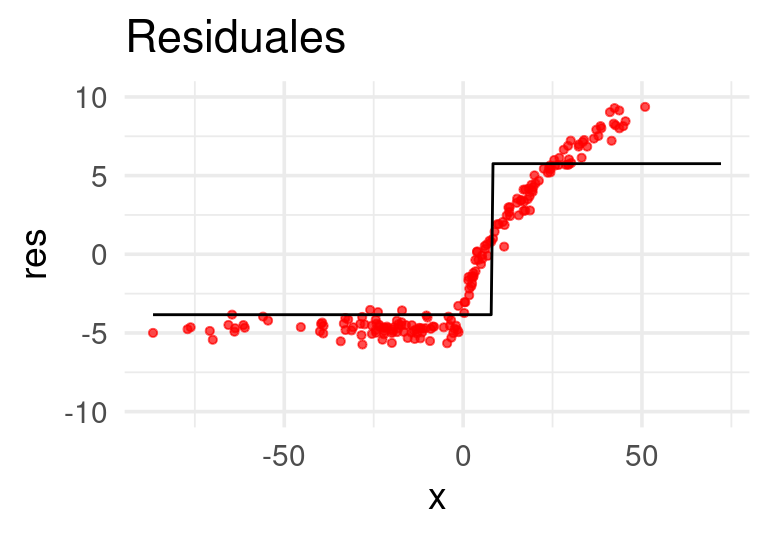
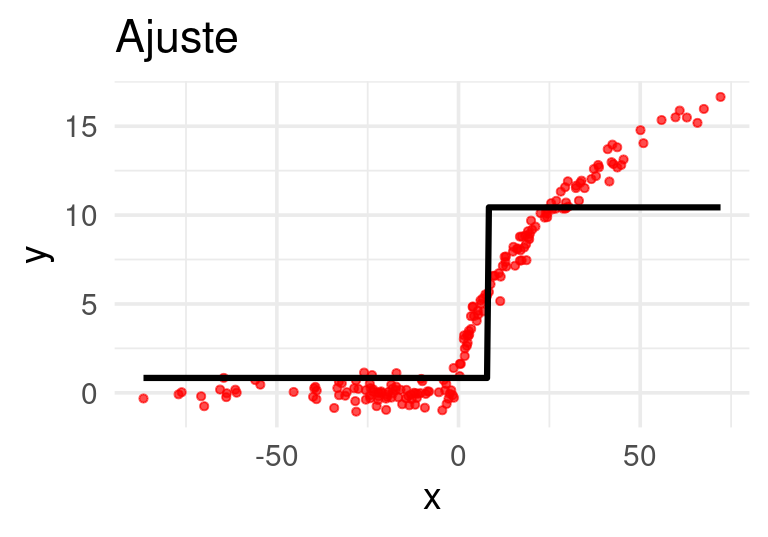
Ajustamos un árbol de regresión a los residuales:
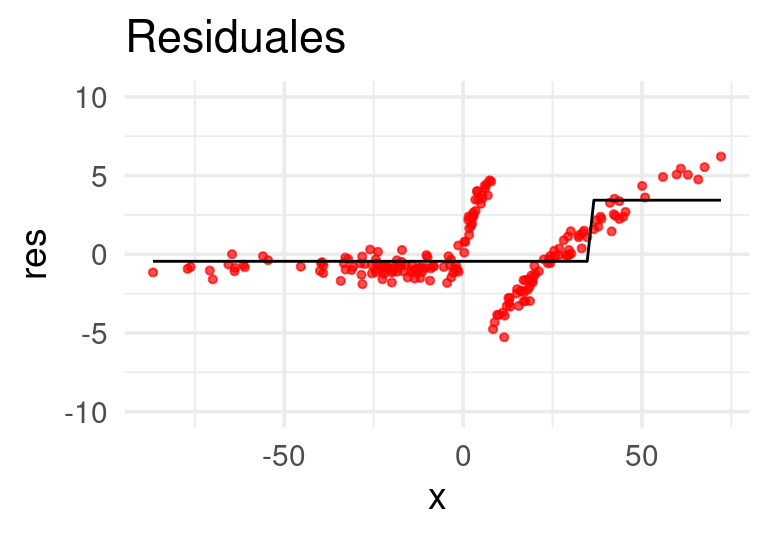
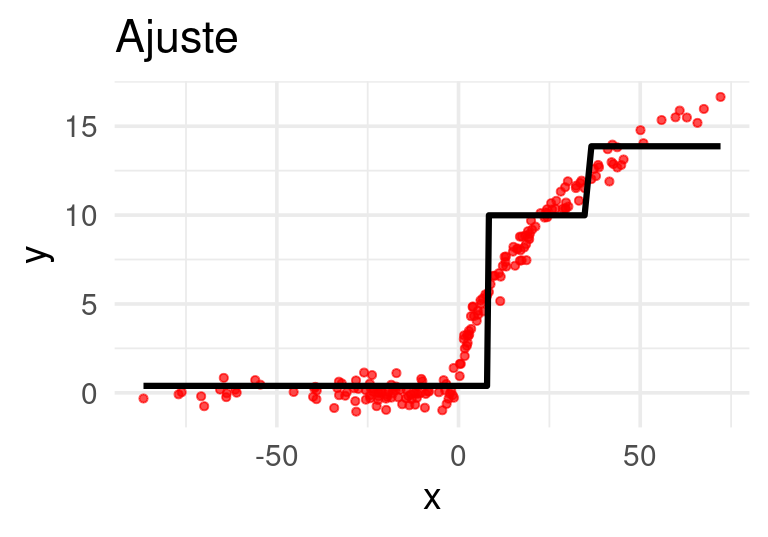
E iteramos:
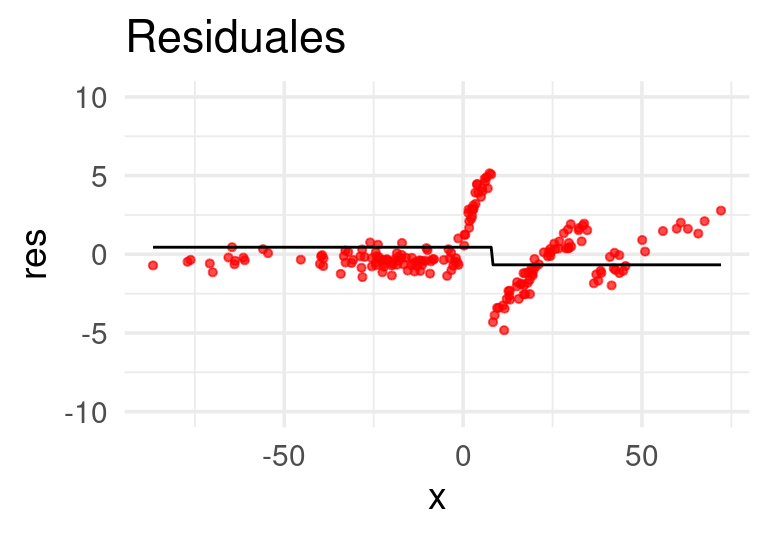
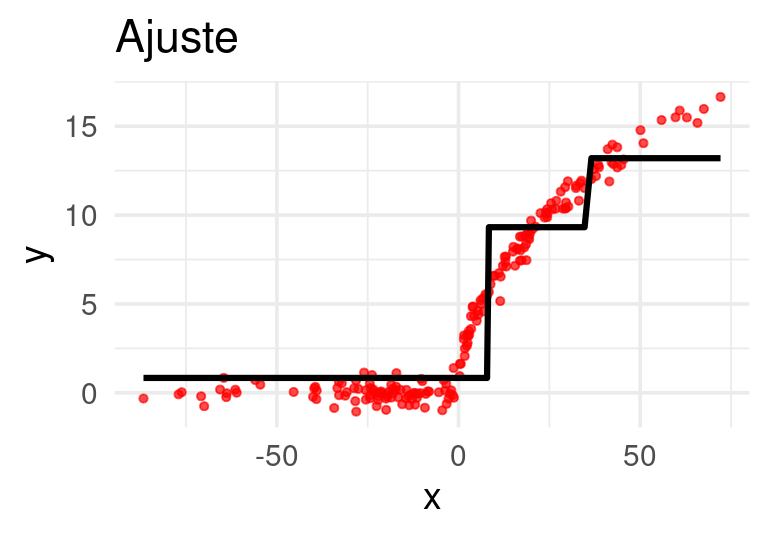
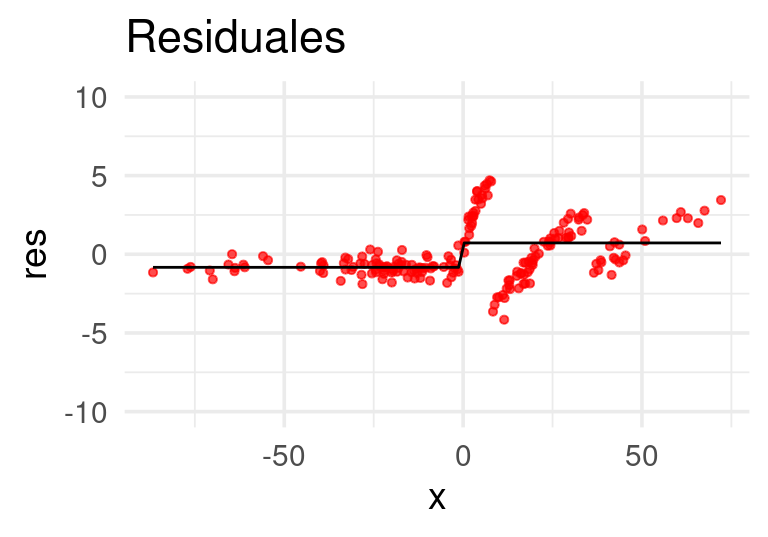
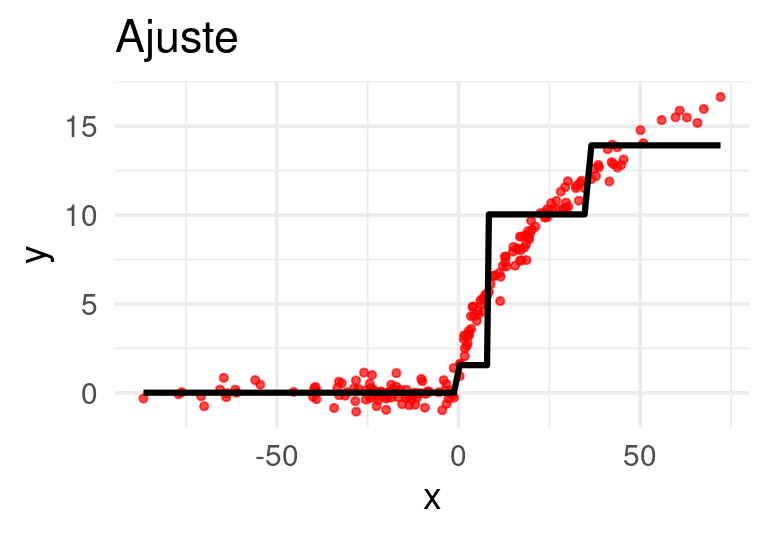
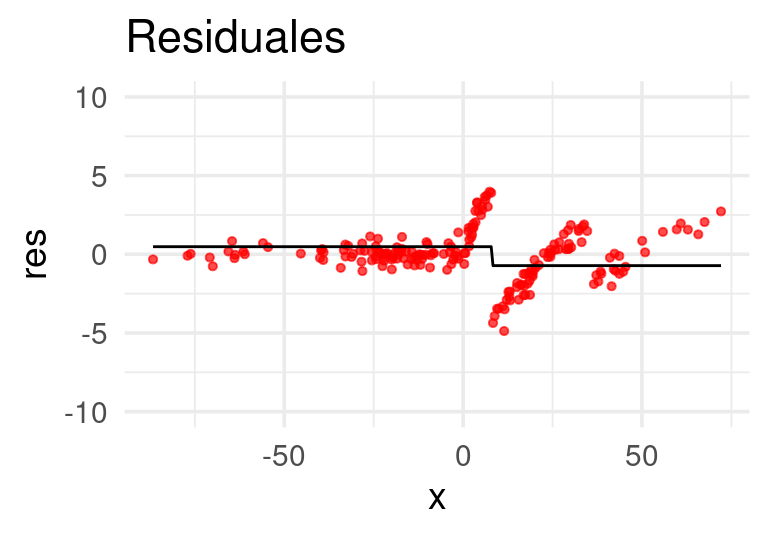
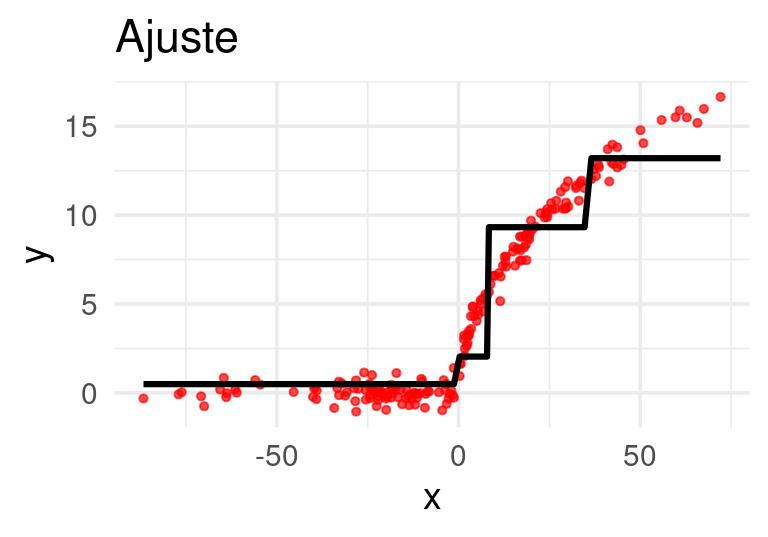
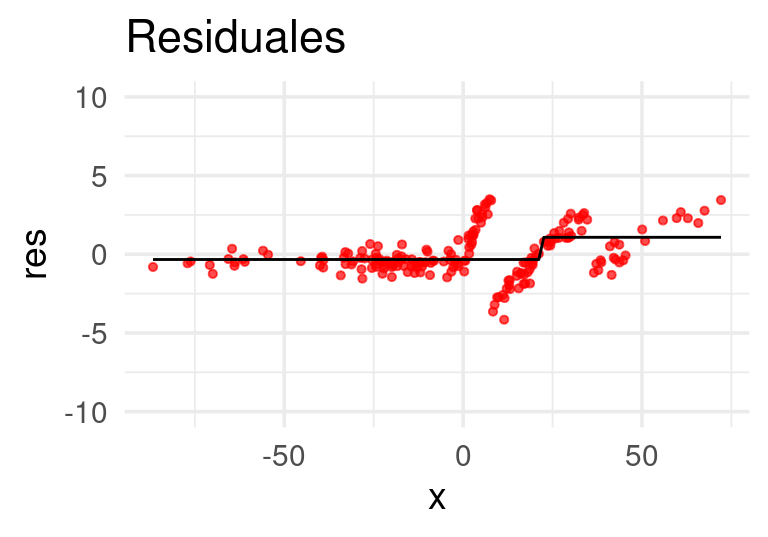
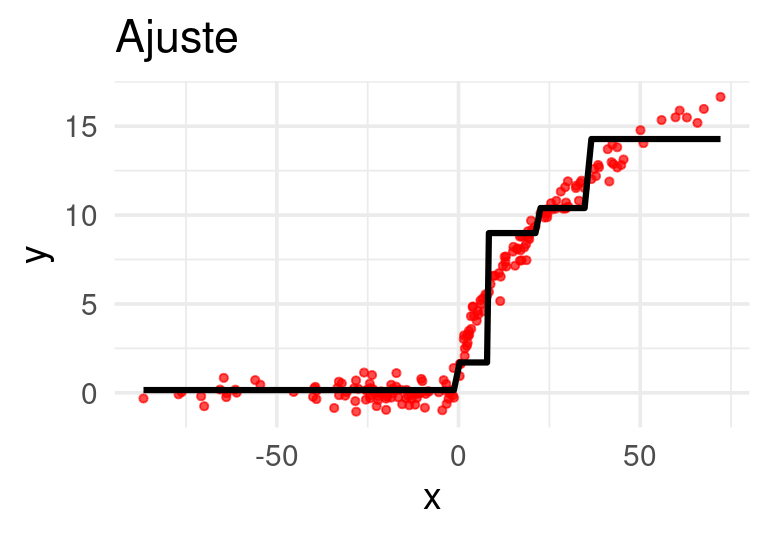
Después de 20 iteraciones obtenemos:
for(j in 1:19){
arboles_fsam <- agregar_arbol(arboles_fsam, dat, plot = FALSE)
}
arboles_fsam <- agregar_arbol(arboles_fsam, dat)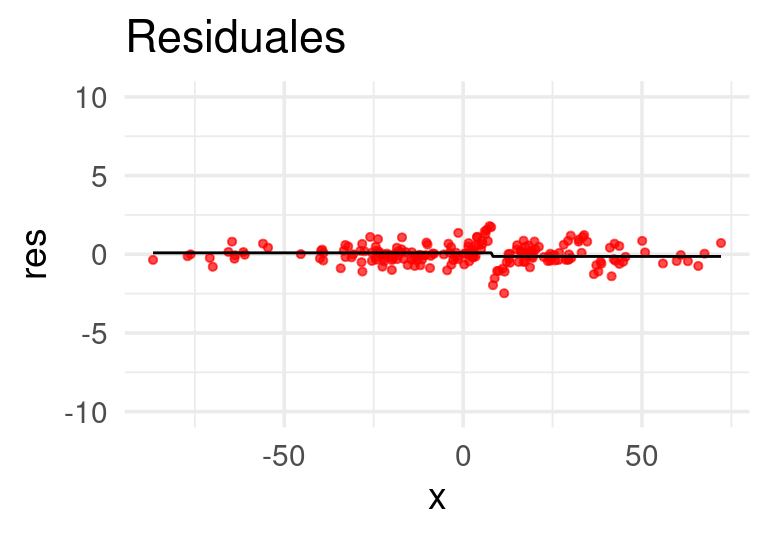
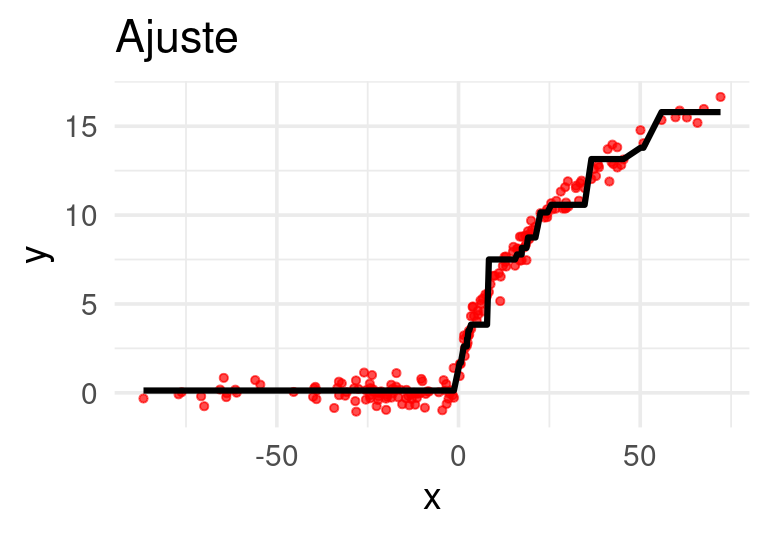
11.4 FSAM para clasificación binaria.
Para problemas de clasificación, no tiene mucho sentido trabajar con un modelo aditivo sobre las probabilidades:
\[p(x) = \sum_{k=1}^m T_k(x),\]
Así que hacemos lo mismo que en regresión logística. Ponemos
\[f(x) = \sum_{k=1}^m T_k(x),\]
y entonces las probabilidades son \[p(x) = h(f(x)),\]
donde \(h(z)=1/(1+e^{-z})\) es la función logística. La optimización de la etapa \(m\) según fsam es
\[\begin{equation} T = argmin_{T} \sum_{i=1}^N L(y^{(i)}, f_{m-1}(x^{(i)}) + T(x^{(i)})) \tag{11.1} \end{equation}\]
y queremos usar la devianza como función de pérdida. Por razones de comparación (con nuestro libro de texto y con el algoritmo Adaboost que mencionaremos más adelante), escogemos usar \[y \in \{1,-1\}\]
en lugar de nuestro tradicional \(y \in \{1,0\}\). En ese caso, la devianza binomial se ve como
\[L(y, z) = -\left [ (y+1)\log h(z) - (y-1)\log(1-h(z))\right ],\] que a su vez se puede escribir como (demostrar):
\[L(y,z) = 2\log(1+e^{-yz})\] Ahora consideremos cómo se ve nuestro problema de optimización:
\[T = argmin_{T} 2\sum_{i=1}^N \log (1+ e^{-y^{(i)}(f_{m-1}(x^{(i)}) + T(x^{(i)}))})\]
Nótese que sólo optimizamos con respecto a \(T\), así que podemos escribir
\[T = argmin_{T} 2\sum_{i=1}^N \log (1+ d_{m,i}e^{- y^{(i)}T(x^{(i)})})\]
Y vemos que el problema es más difícil que en regresión. No podemos usar un ajuste de árbol usual de regresión o clasificación, como hicimos en regresión. No está claro, por ejemplo, cuál debería ser el residual que tenemos que ajustar (aunque parece un problema donde los casos de entrenamiento están ponderados por \(d_{m,i}\)). Una solución para resolver aproximadamente este problema de minimización, es gradient boosting.
11.5 Gradient boosting
La idea de gradient boosting es replicar la idea del residual en regresión, y usar árboles de regresión para resolver (11.1).
Gradient boosting es una técnica general para funciones de pérdida generales.Regresamos entonces a nuestro problema original
\[(\beta_m, b_m) = argmin_{T} \sum_{i=1}^N L(y^{(i)}, f_{m-1}(x^{(i)}) + T(x^{(i)}))\]
La pregunta es: ¿hacia dónde tenemos qué mover la predicción de \(f_{m-1}(x^{(i)})\) sumando el término \(T(x^{(i)})\)? Consideremos un solo término de esta suma, y denotemos \(z_i = T(x^{(i)})\). Queremos agregar una cantidad \(z_i\) tal que el valor de la pérdida \[L(y, f_{m-1}(x^{(i)})+z_i)\] se reduzca. Entonces sabemos que podemos mover la z en la dirección opuesta al gradiente
\[z_i = -\gamma \frac{\partial L}{\partial z}(y^{(i)}, f_{m-1}(x^{(i)}))\]
Sin embargo, necesitamos que las \(z_i\) estén generadas por una función \(T(x)\) que se pueda evaluar en toda \(x\). Quisiéramos que \[T(x^{(i)})\approx -\gamma \frac{\partial L}{\partial z}(y^{(i)}, f_{m-1}(x^{(i)}))\] Para tener esta aproximación, podemos poner \[g_{i,m} = -\frac{\partial L}{\partial z}(y^{(i)}, f_{m-1}(x^{(i)}))\] e intentar resolver \[\begin{equation} \min_T \sum_{i=1}^n (g_{i,m} - T(x^{(i)}))^2, \tag{11.2} \end{equation}\]
es decir, intentamos replicar los gradientes lo más que sea posible. Este problema lo podemos resolver con un árbol usual de regresión. Finalmente, podríamos escoger \(\nu\) (tamaño de paso) suficientemente chica y ponemos \[f_m(x) = f_{m-1}(x)+\nu T(x).\]
Podemos hacer un refinamiento adicional que consiste en encontrar los cortes del árbol \(T\) según (11.2), pero optimizando por separado los valores que T(x) toma en cada una de las regiones encontradas.
11.6 Algoritmo de gradient boosting
Gradient boosting (versión simple)
Inicializar con \(f_0(x) =\gamma\)
Para \(m=0,1,\ldots, M\),
Para \(i=1,\ldots, n\), calculamos el residual \[r_{i,m}=-\frac{\partial L}{\partial z}(y^{(i)}, f_{m-1}(x^{(i)}))\]
Ajustamos un árbol de regresión a la respuesta \(r_{1,m},r_{2,m},\ldots, r_{n,m}\). Supongamos que tiene regiones \(R_{j,m}\).
Resolvemos (optimizamos directamente el valor que toma el árbol en cada región - este es un problema univariado, más fácil de resolver) \[\gamma_{j,m} = argmin_\gamma \sum_{x^{(i)}\in R_{j,m}} L(y^{(i)},f_{m-1}(x^{i})+\gamma )\] para cada región \(R_{j,m}\) del árbol del inciso anterior.
Actualizamos \[f_m (x) = f_{m-1}(x) + \sum_j \gamma_{j,m} I(x\in R_{j,m})\]
- El predictor final es \(f_M(x)\).
11.7 Funciones de pérdida
Para aplicar gradient boosting, tenemos primero que poder calcular el gradiente de la función de pérdida. Algunos ejemplos populares son:
- Pérdida cuadrática: \(L(y,f(x))=(y-f(x))^2\), \(\frac{\partial L}{\partial z} = -2(y-f(x))\).
- Pérdida absoluta (más robusta a atípicos que la cuadrática) \(L(y,f(x))=|y-f(x)|\), \(\frac{\partial L}{\partial z} = signo(y-f(x))\).
- Devianza binomial \(L(y, f(x)) = -\log(1+e^{-yf(x)})\), \(y\in\{-1,1\}\), \(\frac{\partial L}{\partial z} = I(y=1) - h(f(x))\).
- Adaboost, pérdida exponencial (para clasificación) \(L(y,z) = e^{-yf(x)}\), \(y\in\{-1,1\}\), \(\frac{\partial L}{\partial z} = -ye^{-yf(x)}\).
11.7.1 Discusión: adaboost (opcional)
En adaboost usamos la pérdida exponencial. Adaboost es uno de los algoritmos originales para boosting, y no es necesario usar gradient boosting para aplicarlo. La razón es que los árboles de clasificación \(T(x)\) toman valores \(T(x)\in \{-1,1\}\), y el paso de optimización (11.1) de cada árbol queda
\[T = {argmin}_{T} \sum_{i=1}^N e^{-y^{(i)}f_{m-1}(x^{(i)})} e^{-y^{(i)}T(x^{(i)})} \] \[T = argmin_{T} \sum_{i=1}^N d_{m,i} e^{-y^{(i)}T(x^{(i)})} \] De modo que la función objetivo toma dos valores: Si \(T(x^{i})\) clasifica correctamente, entonces \(e^{-y^{(i)}T(x^{(i)})}=e^{-1}\), y si clasifica incorrectamente \(e^{-y^{(i)}T(x^{(i)})}=e^{1}\). Podemos entonces encontrar el árbol \(T\) construyendo un árbol usual pero con datos ponderados por \(d_{m,i}\), donde buscamos maximizar la tasa de clasificación correcta (puedes ver más en nuestro libro de texto, o en (Hastie, Tibshirani, and Friedman 2017).
¿Cuáles son las consecuencias de usar la pérdida exponencial? Una es que perdemos la conexión con los modelos logísticos e interpretación de probabilidad que tenemos cuando usamos la devianza. Sin embargo, son similares: compara cómo se ve la devianza (como la formulamos arriba, con \(y\in\{-1,1\}\)) con la pérdida exponencial.
Ejemplo: precios de casas
Consideramos el ejemplo de precio de casas. Haremos un mínimo de preprocesamiento:
library(xgboost)
add_underscore <- function(string){
str_replace_all(string, " * ", "_")
}
entrena_casas_tbl <- read_csv("../examen/concurso/casas_entrena.csv", quoted_na = FALSE) %>%
mutate(log_precio = log(1 + SalePrice)) %>%
rename_all(add_underscore) %>%
mutate(Garage_Qual = ifelse(Garage_Qual == "Ex", "Gd", Garage_Qual)) %>%
mutate(Garage_Qual = ifelse(Garage_Qual == "Po", "Fa", Garage_Qual)) %>%
mutate(Heating_QC = ifelse(Heating_QC == "Po", "Fa", Heating_QC)) %>%
mutate(Kitchen_Qual = ifelse(Kitchen_Qual == "Po", "TA", Kitchen_Qual)) %>%
mutate(Bsmt_Qual = ifelse(Bsmt_Qual == "Po", "TA", Bsmt_Qual)) %>%
filter(Sale_Condition == "Normal") %>%
select(-Sale_Type, -Sale_Condition, -Mo_Sold, -SalePrice)
receta_casas <- recipe(log_precio ~ ., data = entrena_casas_tbl ) %>%
step_other(all_nominal(), threshold = 0.05) %>%
step_unknown(all_nominal()) %>%
step_nzv(all_nominal()) %>% # varianza cero
step_dummy(all_nominal()) %>%
prep()Vamos a usar para este ejemplo la interfaz de xgboost directamente.
y_entrena <- entrena_casas_tbl$log_precio
x_entrena <- juice(receta_casas) %>% select(-log_precio) %>% as.matrix
dim(x_entrena)## [1] 1209 153# convertir a clase apropiada para xgboost
d_entrena <- xgb.DMatrix(data = x_entrena, label= y_entrena)Usaremos el paquete xgboost que usa la librería xgboost.
Fijaremos el número de árboles en 100, de profundidad 4, y estimamos el error con validación cruzada. La salida muestra el error de entrenamiento y el estimado con validacion cruzada:
params = list(
objective = "reg:squarederror",
eta = 1, # tamaño de paso
max_depth = 1, # profundidad de árboles
colsample_bynode = 0.2, # prop de variables usadas para candidatos
lambda = 0)
set.seed(812) # para validación cruzada
mod_boost_cv <- xgb.cv(params = params,
data = d_entrena,
nfold = 10,
nrounds = 100, # número de árboles
predictions = TRUE,
print_every_n = 10)## [1] train-rmse:0.297021+0.012043 test-rmse:0.296629+0.033154
## [11] train-rmse:0.182981+0.006592 test-rmse:0.195358+0.028811
## [21] train-rmse:0.151705+0.006627 test-rmse:0.170349+0.014691
## [31] train-rmse:0.131730+0.004016 test-rmse:0.152364+0.013360
## [41] train-rmse:0.120359+0.003852 test-rmse:0.141987+0.009737
## [51] train-rmse:0.111804+0.003005 test-rmse:0.133493+0.010600
## [61] train-rmse:0.105192+0.003305 test-rmse:0.128713+0.008400
## [71] train-rmse:0.100025+0.002927 test-rmse:0.126196+0.009837
## [81] train-rmse:0.095931+0.002860 test-rmse:0.122318+0.009139
## [91] train-rmse:0.092706+0.002541 test-rmse:0.120087+0.010410
## [100] train-rmse:0.090330+0.002264 test-rmse:0.118227+0.009432transformar_eval <- function(mod_boost_cv){
eval_tbl <- mod_boost_cv$evaluation_log %>%
gather(variable, valor, -iter) %>%
separate(variable, into = c("tipo", "metrica", "res")) %>%
spread(res, valor)
eval_tbl
}
graficar_vc <- function(eval_tbl){
error_entrena <- eval_tbl %>% filter(tipo == "train") %>% pull(mean) %>% last
error_val <- eval_tbl %>% filter(tipo == "test") %>% pull(mean) %>% last
sd_error_val <- eval_tbl %>% filter(tipo == "test") %>% pull(std) %>% last
sprintf("Error entrena: %.2f, Error valida: %.2f, ee valida: %.2f",
error_entrena, error_val, sd_error_val) %>% print
ggplot(eval_tbl, aes(x = iter, y = mean, ymin = mean - std, ymax = mean + std,
colour = tipo)) +
scale_y_log10(breaks = c(0.01, 0.1, 0.2, 0.4, 0.8, 1.6, 3.2)) +
geom_point() + geom_linerange()
}
mod_boost_cv %>% transformar_eval() %>% graficar_vc()## [1] "Error entrena: 0.09, Error valida: 0.12, ee valida: 0.01"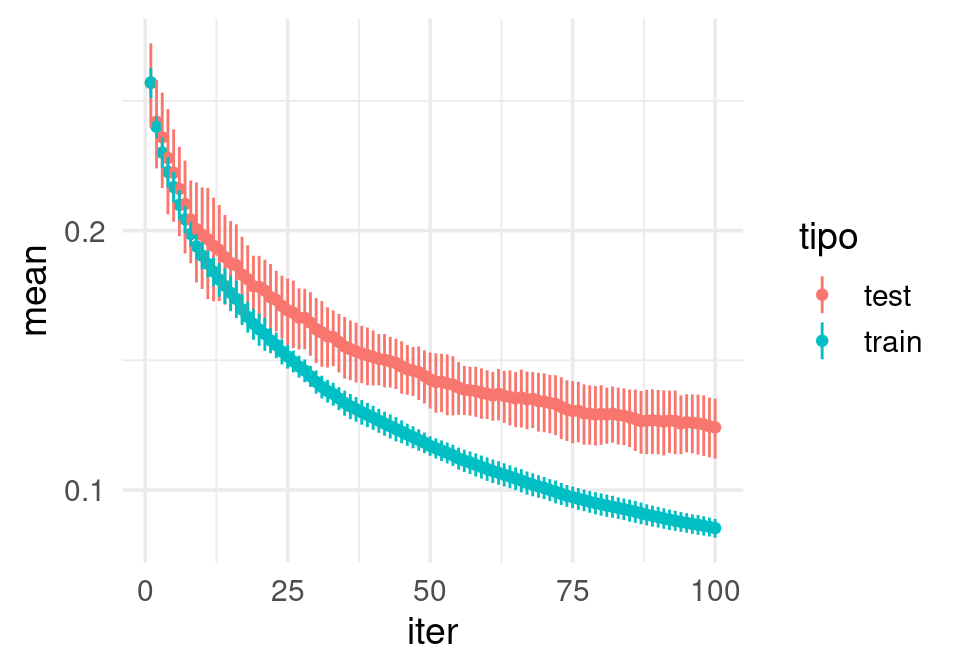
Mostraremos ahora cómo controlar el proceso de optimización para obtener buen desempeño predictivo.
11.8 Afinación para Gradient Boosting
Hay algunas adiciones al algoritmo de gradient boosting que podemos usar para mejorar el desempeño, además del número de árboles y su profundidad. Los dos métodos que comunmente se usan son encogimiento (shrinkage), que es una especie de tasa de aprendizaje, y submuestreo, donde construimos cada árbol adicional usando una submuestra de la muestra de entrenamiento.
Ambas podemos verlas como técnicas de regularización, que limitan sobreajuste producido por el algoritmo agresivo de boosting.
11.8.1 Tasa de aprendizaje (shrinkage)
Funciona bien modificar el algoritmo usando una tasa de aprendizaje \(0<\eta<1\): \[f_m(x) = f_{m-1}(x) + \eta \sum_j \gamma_{j,m} I(x\in R_{j,m})\]
Este parámetro sirve como una manera de evitar sobreajuste rápido cuando construimos los predictores. Si este número es muy alto, podemos sobreajustar rápidamente con pocos árboles, y terminar con predictor de varianza alta. Si este número es muy bajo, puede ser que necesitemos demasiadas iteraciones para llegar a buen desempeño. Este, junto el número de iteraciones, es de los parámetros más importantes.
Igualmente se prueba con varios valores de \(0<\eta<1\) (típicamente \(\eta<0.1\)) para mejorar el desempeño en validación. Nota: cuando hacemos \(\eta\) más chica, es necesario hacer \(M\) más grande (correr más árboles) para obtener desempeño óptimo.
Veamos que efecto tiene en nuestro ejemplo. Reducimos considerablemente la tasa de aprendizaje:
params = list(
objective = "reg:squarederror",
eta = 0.1, # tamaño de paso
max_depth = 1, # profundidad de árboles
colsample_bynode = 0.2, # muestreo de columnas
lambda = 0)
set.seed(812) # para validación cruzada
mod_boost_cv <- xgb.cv(params = params,
data = d_entrena,
nfold = 10,
nrounds = 1200, # número de árboles
print_every_n = 100)## [1] train-rmse:10.356586+0.001909 test-rmse:10.356710+0.019299
## [101] train-rmse:0.114871+0.000889 test-rmse:0.128501+0.016606
## [201] train-rmse:0.094896+0.000856 test-rmse:0.111576+0.012481
## [301] train-rmse:0.088806+0.000995 test-rmse:0.106664+0.011272
## [401] train-rmse:0.085466+0.001140 test-rmse:0.104159+0.010930
## [501] train-rmse:0.083166+0.001232 test-rmse:0.102628+0.010794
## [601] train-rmse:0.081427+0.001259 test-rmse:0.101565+0.010546
## [701] train-rmse:0.080033+0.001257 test-rmse:0.100834+0.010585
## [801] train-rmse:0.078867+0.001242 test-rmse:0.100280+0.010599
## [901] train-rmse:0.077864+0.001222 test-rmse:0.099741+0.010573
## [1001] train-rmse:0.076983+0.001206 test-rmse:0.099424+0.010623
## [1101] train-rmse:0.076197+0.001194 test-rmse:0.099207+0.010584
## [1200] train-rmse:0.075495+0.001184 test-rmse:0.098986+0.010589Obsérvese que podemos obtener un mejor resultado de validación afinando la tasa de aprendizaje. Cuando es muy grande, el modelo rápidamente sobreajusta cuando agregamos árboles. Si la tasa es demasiado chica, podemos tardar mucho en llegar a un predictor de buen desempeño.
11.8.2 Submuestreo
Funciona bien construir cada uno de los árboles con submuestras de la muestra de entrenamiento, como una manera adicional de reducir varianza al construir nuestro predictor (esta idea es parecida a la de los bosques aleatorios, aquí igualmente perturbamos la muestra de entrenamiento en cada paso para evitar sobreajuste). Adicionalmente, este proceso acelera considerablemente las iteraciones de boosting, y en algunos casos sin penalización en desempeño.
En boosting generalmente se toman submuestras (una fracción de alrededor de 0.5 de la muestra de entrenamiento, pero puede ser más chica para conjuntos grandes de entrenamiento) sin reemplazo.
Este parámetro también puede ser afinado con muestra de validación o validación cruzada.
params = list(
objective = "reg:squarederror",
eta = 0.05, # tamaño de paso
max_depth = 1, # profundidad de árboles
subsample = 0.5, # submuestrear casos
colsample_bynode = 0.2,
lambda = 0)
ajustar_mod <- function(d_entrena, verbose = 0, nrounds = 400, params, every_n = 100){
mod_boost_cv <- xgb.cv(params = params,
data = d_entrena,
nfold = 10,
nrounds = nrounds, # número de árboles
predictions = TRUE,
print_every_n = every_n,
nthread = 10, # modificar según recursos
verbose = verbose)
eval_tbl <- mod_boost_cv$evaluation_log %>%
gather(variable, valor, -iter) %>%
separate(variable, into = c("tipo", "metrica", "res")) %>%
spread(res, valor)
eval_tbl
}
res <- ajustar_mod(d_entrena, verbose = 1, nrounds = 1200, params = params)## [1] train-rmse:10.931461+0.002144 test-rmse:10.931511+0.019761
## [101] train-rmse:0.165179+0.001227 test-rmse:0.173350+0.015250
## [201] train-rmse:0.112584+0.001127 test-rmse:0.124741+0.010276
## [301] train-rmse:0.099030+0.001073 test-rmse:0.111993+0.008835
## [401] train-rmse:0.092722+0.001110 test-rmse:0.106503+0.008477
## [501] train-rmse:0.089003+0.001175 test-rmse:0.103542+0.008893
## [601] train-rmse:0.086492+0.001165 test-rmse:0.102124+0.009598
## [701] train-rmse:0.084515+0.001146 test-rmse:0.100899+0.009914
## [801] train-rmse:0.082915+0.001111 test-rmse:0.099841+0.010004
## [901] train-rmse:0.081615+0.001072 test-rmse:0.099438+0.010139
## [1001] train-rmse:0.080491+0.001085 test-rmse:0.098971+0.010171
## [1101] train-rmse:0.079468+0.001115 test-rmse:0.098938+0.010216
## [1200] train-rmse:0.078599+0.001136 test-rmse:0.098726+0.010132En este ejemplo, podemos reducir el tiempo de ajuste usando una fracción de submuestro de 0.5, con quizá algunas mejoras en desempeño.
Ahora veamos los dos parámetros actuando en conjunto, junto con el número de iteraciones:
df_params <- list(objective = "reg:squarederror",
eta = c(0.01, 0.05, 0.1, 0.25, 0.5),
subsample = c(0.1, 0.5, 1.0),
colsample_bynode = 0.2,
maxdepth = 1, lambda = 0) %>% cross_df
df_params <- df_params %>%
mutate(eval_log = pmap(df_params, ~ ajustar_mod(d_entrena, nrounds = 250, params = list(...))))
df_params_u <- df_params %>% unnest(cols = c(eval_log))g_1 <- ggplot(df_params_u %>% filter(iter > 5),
aes(x = iter, y = mean, colour = tipo)) +
facet_grid(eta~subsample,
labeller = labeller(.rows = label_both, .cols = label_both)) +
geom_hline(yintercept = 0.1) + geom_point() + scale_y_log10()
g_1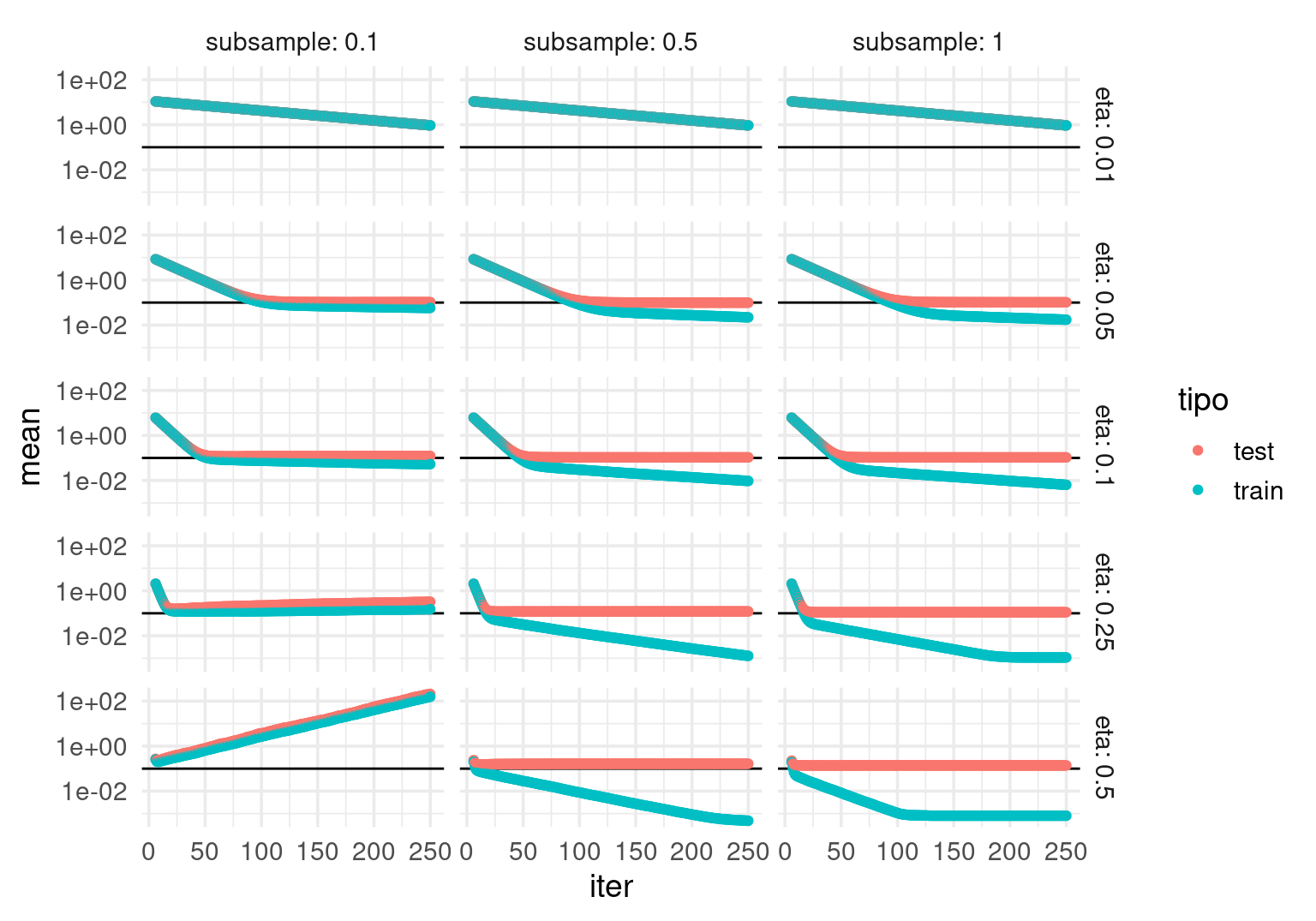
df_params_u %>% filter(iter == 250, tipo == "test", eta < 0.5) %>%
ggplot(aes(x = eta, y = mean, ymin = mean - std, ymax = mean + std,
colour = factor(subsample))) +
geom_point() + geom_line() + geom_linerange() +
scale_y_log10() + scale_x_log10() + ylab("RECML (validación cruzada 10)")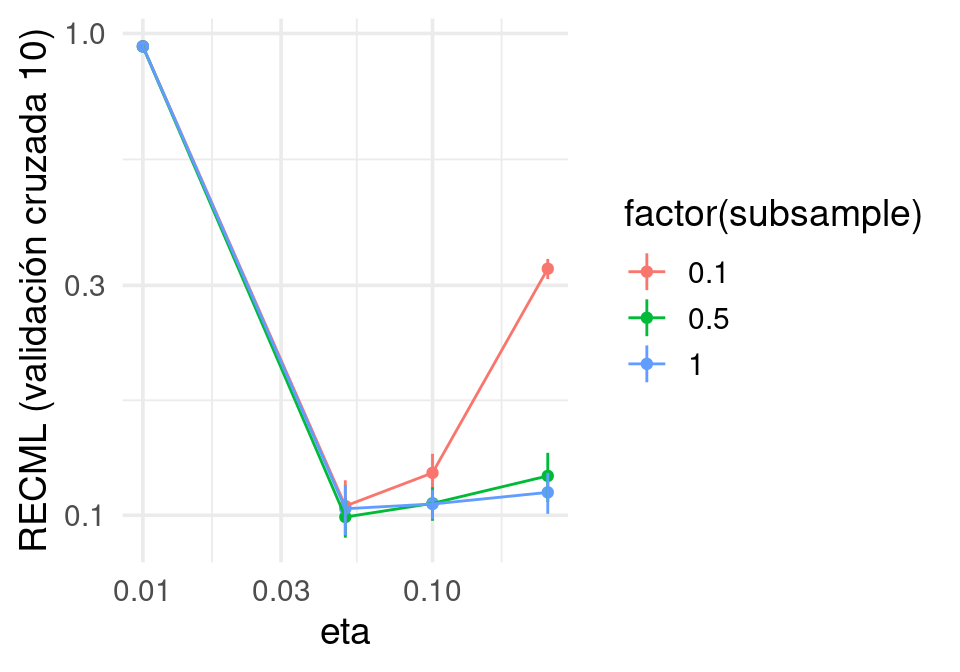
Nótese que:
- Valores altos de \(\eta\) junto con valores muy chicos de subsample producen que el optimizador no funcione bien.
- Valores altos de \(\eta\) pueden producir modelos con más sobreajuste.
- Valores bajos de \(\eta\) requieren más iteraciones para reducir el error, pero pueden reducir el sobreajuste.
11.8.3 Tamaño de árboles
Los árboles se construyen de tamaño fijo \(J\), donde \(J\) es el número de cortes. Usualmente \(J=1,2,\ldots, 10\), y es un parámetro que hay que elegir. \(J\) más grande permite interacciones de orden más alto entre las variables de entrada. Podemos por ejemplo comenzar probando al azar de la siguiente rejilla:
grid_tbl <- list(objective = "reg:squarederror",
eta = c(0.01, 0.05),
subsample = c(0.5, 0.9),
maxdepth = c(2, 4, 8),
colsample_by_node = c(0.1, 0.3),
lambda = c(0.1, 1, 10)) %>% cross_df
set.seed(883)
# hacemos búsqueda aleatoria (haz size más grande)
subgrid_tbl <- sample_n(grid_tbl, size = 20) # busqueda aleatoria
eval_log <- pmap(subgrid_tbl, ~ ajustar_mod(d_entrena,
nrounds = 2000, params = list(...)))
subgrid_tbl <- subgrid_tbl %>% mutate(eval_log = eval_log)
eval_tbl <- subgrid_tbl %>% unnest() %>%
filter(iter == 500, tipo == "test") %>%
arrange(mean)## Warning: `cols` is now required when using unnest().
## Please use `cols = c(eval_log)`## # A tibble: 20 x 7
## eta subsample maxdepth colsample_by_node lambda mean std
## <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 0.05 0.5 4 0.1 0.1 0.0976 0.0115
## 2 0.05 0.5 8 0.3 0.1 0.0976 0.0128
## 3 0.05 0.5 4 0.1 1 0.0977 0.00739
## 4 0.05 0.5 2 0.1 0.1 0.0992 0.00984
## 5 0.05 0.9 4 0.3 1 0.0993 0.0102
## 6 0.05 0.9 8 0.3 0.1 0.101 0.00990
## 7 0.05 0.9 2 0.3 0.1 0.101 0.0105
## 8 0.05 0.9 8 0.1 1 0.101 0.00832
## 9 0.05 0.9 8 0.3 10 0.102 0.0166
## 10 0.05 0.5 4 0.3 10 0.102 0.0154
## 11 0.05 0.5 2 0.3 10 0.103 0.00913
## 12 0.01 0.5 4 0.1 0.1 0.127 0.0109
## 13 0.01 0.9 8 0.1 0.1 0.129 0.0107
## 14 0.01 0.5 2 0.3 1 0.138 0.0175
## 15 0.01 0.9 8 0.3 1 0.139 0.0111
## 16 0.01 0.5 4 0.3 1 0.140 0.00936
## 17 0.01 0.9 4 0.3 10 0.164 0.0143
## 18 0.01 0.9 4 0.1 10 0.165 0.0173
## 19 0.01 0.9 8 0.3 10 0.167 0.0186
## 20 0.01 0.5 8 0.1 10 0.177 0.0129Observación: muchas veces es necesario correr más iteraciones de las que en primera instancia planeas, especialmente cuando el valor de \(\eta\) es chico. En estas primeras corridas no necesariamente es bueno descartar combinaciones de parámetros con \(\eta\) relativamente chica y que son prometedores. Experimentar con el número de iteraciones es buena idea, pues muchas veces el predictor mejora considerablemente.
Usando esta información podemos seleccionar un juego de parámetros y correr más iteraciones. Después de algunos experimentos adicionales, obtenemos:
set.seed(121)
params = list(
objective = "reg:squarederror",
eta = 0.0015, # tamaño de paso
max_depth = 3, # profundidad de árboles
min_child_weight = 1,
colsample_bynode = 0.2,
subsample = 0.4,
lambda = 0.05)
res <- ajustar_mod(d_entrena, verbose = 1, nrounds = 25000, params = params,
every_n = 1000)## [1] train-rmse:11.489177+0.004717 test-rmse:11.489009+0.042778
## [1001] train-rmse:2.568239+0.000942 test-rmse:2.568694+0.025505
## [2001] train-rmse:0.583500+0.000217 test-rmse:0.586449+0.017298
## [3001] train-rmse:0.157546+0.000487 test-rmse:0.168898+0.012410
## [4001] train-rmse:0.085962+0.000773 test-rmse:0.106093+0.010488
## [5001] train-rmse:0.074832+0.000818 test-rmse:0.098281+0.010132
## [6001] train-rmse:0.070079+0.000774 test-rmse:0.095780+0.010196
## [7001] train-rmse:0.066557+0.000730 test-rmse:0.094439+0.010277
## [8001] train-rmse:0.063628+0.000695 test-rmse:0.093515+0.010376
## [9001] train-rmse:0.061073+0.000662 test-rmse:0.092828+0.010463
## [10001] train-rmse:0.058778+0.000656 test-rmse:0.092251+0.010499
## [11001] train-rmse:0.056698+0.000620 test-rmse:0.091879+0.010545
## [12001] train-rmse:0.054793+0.000601 test-rmse:0.091601+0.010625
## [13001] train-rmse:0.053018+0.000581 test-rmse:0.091332+0.010649
## [14001] train-rmse:0.051380+0.000566 test-rmse:0.091143+0.010697
## [15001] train-rmse:0.049834+0.000547 test-rmse:0.090976+0.010733
## [16001] train-rmse:0.048397+0.000538 test-rmse:0.090864+0.010756
## [17001] train-rmse:0.047025+0.000520 test-rmse:0.090802+0.010729
## [18001] train-rmse:0.045731+0.000509 test-rmse:0.090741+0.010728
## [19001] train-rmse:0.044505+0.000500 test-rmse:0.090691+0.010733
## [20001] train-rmse:0.043346+0.000481 test-rmse:0.090657+0.010722
## [21001] train-rmse:0.042240+0.000470 test-rmse:0.090631+0.010744
## [22001] train-rmse:0.041176+0.000456 test-rmse:0.090587+0.010758
## [23001] train-rmse:0.040169+0.000448 test-rmse:0.090585+0.010750
## [24001] train-rmse:0.039198+0.000435 test-rmse:0.090588+0.010778
## [25000] train-rmse:0.038269+0.000423 test-rmse:0.090559+0.010793Finalmente podemos guardar el modelo en un formato estándar (R, Python, etc):
11.9 Otros parámetros
También es posible usar hiperparámetros adicionales:
- Seleccionar variables al azar para construir cada árbol o seleccionar variables al azar por nodo (como en bosques aleatorios)
- Número mínimo de casos por nodo
- Regularización L1 (arriba sólo usamos L2)
11.10 Algoritmo xgboost
El algoritmo xgboost tiene optimizaciones e ideas adicionales para mejorar desempeño, y su implementación estándar es una libraría robusta.
Aquí discutiremos algunas diferencias del algoritmo original de gradient boosting y esta implementación.
Regularización por complejidad y L2
En el algoritmo FSAM, buscábamos minimizar (encontrando un árbol que agregamos al predictor de la iteración anterior):
\[\min_{T} \sum_{i=1}^N L(y^{(i)}, f_{m-1}(x^{(i)}) + T(x^{(i)}))\] En xgboost, consideramos en lugar de esto la pérdida regularizada:
\[\min_{T} \sum_{i=1}^N L(y^{(i)}, f_{m-1}(x^{(i)}) + T(x^{(i)})) + \Omega(T)\] donde \[\Omega(T) = \gamma |T| + \lambda \sum_t w_t ^2\] donde las \(w_t\) son los valores de \(T\) en cada una de sus nodos terminales. Se usa entonces una penalización costo-complejidad como en árboles CART (el término de \(\gamma\)), junto con una penalización L2 sobre las predicciones del nuevo árbol ajustado, donde \(T(x^{(i)}) = w_{t(i)}\).
Paso de optimización cuadrático
En xgboost, en lugar de usar solo el gradiente para hacer cada paso, se utiliza una aproximación de segundo orden a la función de pérdida y se optimiza analíticamente:
\[L(y^{(i)}, f_{m-1}(x^{(i)}) + T(x^{(i)}))\approx L(y^{(i)}, f_{m-1}(x^{(i)})) + g_iT(x^{(i)}) + \frac{1}{2}h_i (T(x^{(i)}))^2\]
donde \(g_i\) es el gradiente y \(h_i\) es la segunda derivada de la función de pérdida. El primer término del lado derecho de esta ecuación es constante, y dada una estructura de árbol dada, es posible encontrar analíticamente los pesos \(T(x^{(i)})\) que minimizan el lado derecho de esta ecuación. Este enfoque parece mejorar la velocidad y calidad de los predictores resultantes. Para escoger los cortes se seleccionan variables y puntos de corte usando de manera miope con este criterio (Chen and Guestrin 2016).
Otras optimizaciones de xgboost
Adicionalmente, xgboost y implementaciones modernas de boosting están diseñadas para ser escaladas a datos más grandes. Esto incluye paralelismo, manejo eficiente de memoria, posibilidad de usar GPUs para el entrenamiento, y aproximaciones eficientes para encontrar los cortes para cada estructura (Chen and Guestrin 2016) de árbol.